机器人控制原理课程设计（两个简单系统的设计）

摘 要

题目一为数控六角车床控制系统，设计校正装置，采用期望特性法，使系统达到所给要求。

题目二为直流电机控制系统，设计校正装置，采用PID方法，使系统达到所给要求。

关键词：校正装置，期望特性法，PID

Abstract

The first topic is the control system of NC hexagonal lathe. The design of corrector adopts the expected characteristic method to make the system meet the given requirements.

The second topic is the DC motor control system, design the correction device, and use the PID method to make the system meet the given requirements.

Keywords: Corrector, Expected characterization method, PID

目 录

摘要 ………………………………………………………………………………..Ⅰ

Abstract ……………………………………………………………………………. Ⅰ

第1章 总体方案论证

1.1 数控六角车床控制系统……………………………………………………….1

1.2 直流电机控制系统…………………………………………………………….1

第2章 人工设计

2.1 数控六角车床控制系统……………………………………………………….2

2.2 直流电机控制系统…………………………………………………………….4

第3章 计算机辅助设计

3.1 数控六角车床控制系统……………………………………………………….6

3.2 直流电机控制系统…………………………………………………………….8

第4章 总结收获…………………………………………………………………12

第1章 总体方案论证

1.1 数控六角车床控制系统

​ 题目技术要求为系统阻尼系数达到0.7，超调量小于5%，斜坡响应的稳态误差为2.5%。

​ 根据高阶系统

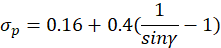
​ 可知，按此经验公式，超调量最低也是16%，远大于题目所要求的5%，常规的频域校正方法不适用。

因此决定采用期望特性的校正方法，来设计校正装置的传递函数。

​ 根据所给指标，先得到期望的二阶系统，再用期望的二阶系统除以系统固有的传递函数，得到校正装置的传递函数。

1.2 直流电机控制系统

​ 直流电机控制系统技术要求为阶跃响应调整时间小于0.6s，超调量小于5%。超调量小于5%，显然依然不能使用高阶系统经验公式求得。

​ 因此结合实际，准备采用PID进行控制，PID控制是在过程控制中，按偏差的比例（P）、积分（I）和微分（D）进行控制的一种方法。

​ 本文准备借用Matlab中的pidtool进行pid参数的获取。通过PID参数整定得到校正装置函数，从而得到最终的传递函数。

第2章 人工设计

2.1 数控六角车床控制系统

​ 假设目标传递函数为二阶系统，根据

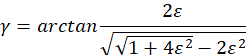
​ 求得阻尼系数0.7时所对应的相角裕度约为54.73°，系统稳定，再根据

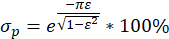
​ 求得阻尼系数0.7时所对应的超调量约为4.6%，小于所要求的5%，再根据系统斜坡响应的稳态误差求得目标系统理想增益k = 40，再根据二阶系统开环传递函数标准形式

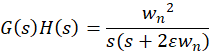
​ 求得期望二阶系统阻尼系数为0.7，无阻尼自然频率,即

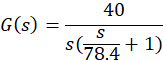
​ 再由题意得出系统固有传递函数

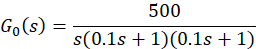
​ 使用期望特性法，用目标开环传函除以当前开环传函，得到校正装置传递函数，意即

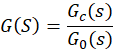
​ 得到校正装置传递函数

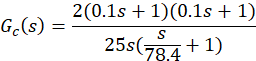
​ 可见校正装置由两个微分环节、一个积分环节及一个惯性环节组成。

2.2 直流电机控制系统

​ 首先进行对开环传递函数的求取，得

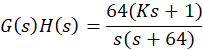
​ 先假定传递环数中K = 1，然后将其导入MATLAB中pidtool中进行可视化调整，经过不断调整，决定将K值设为0.1，得到PID参数：

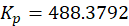
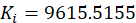
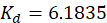
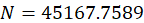
​ 校正装置的传递函数为

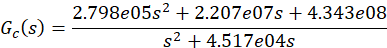
​ 从而得到整个系统的开环传递函数

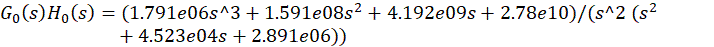
第3章 计算机辅助设计

3.1 数控六角车床控制系统

​ 在simulink中搭建系统如图

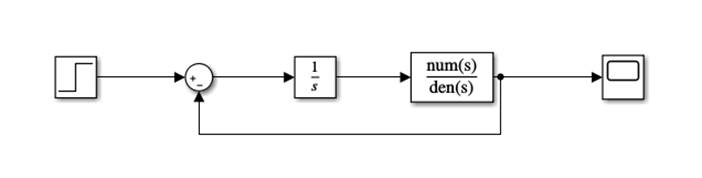
​ 图3-1 数控六角车床控制系统仿真图

​ 仿真后得到的阶跃响应曲线如图

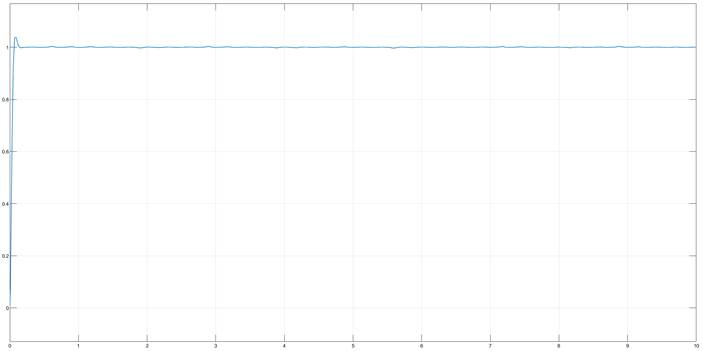
​ 图3-2 数控六角车床控制系统阶跃响应图

​ 系统校正前后及校正装置的Bode图如图：

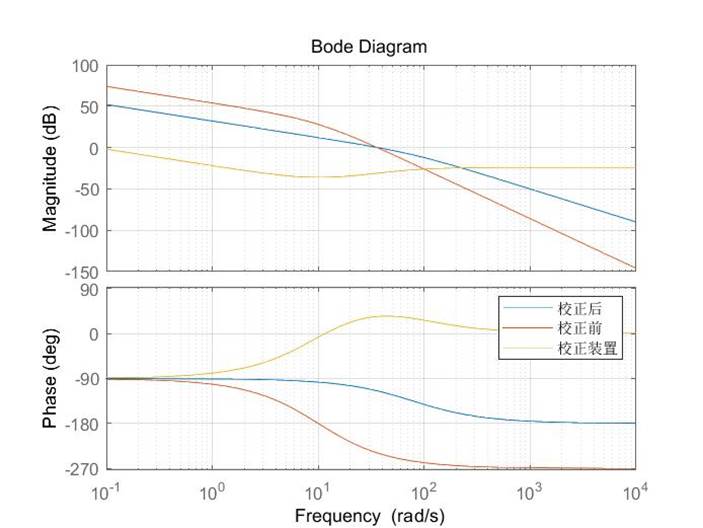
​ 图3-3 数控六角车床控制系统Bode图

​ 图3-4 数控六角车床控制系统simulink中阶跃响应图

​ 由图易求得系统校正后超调量为3.8%，小于5%，满足要求，且整个过程相角裕度为正，系统稳定。

代码解释

得到目标二阶系统开环传递函数  

num =  [40];  

den =  [1/78.4,1,0]; 

sys =  tf(num,den)     

得到系统固有开环传递函数  

num2 =  [500];  

den2 =  [0.01,0.2,1,0];  

sys2 =  tf(num2,den2)     

得到系统校正装置开环传递函数  

num3 = [0.02,0.4,2]; 

den3 =  [25/78.4,25,0];

sys3 =  tf(num3,den3)    

在图窗1绘制系统校正后的阶跃响应图

sysj1 =  feedback(sys,1) 

figure(1)  

step(sysj1)     

在图窗2绘制校正前后及校正装置的Bode图 

 figure(2)  bode(sys)  hold;  

bode(sys2) 

bode(sys3) 

legend('校正后','校正前','校正装置')  

grid on;     

3.2 直流电机控制系统

​ 在simulink中搭建系统如图

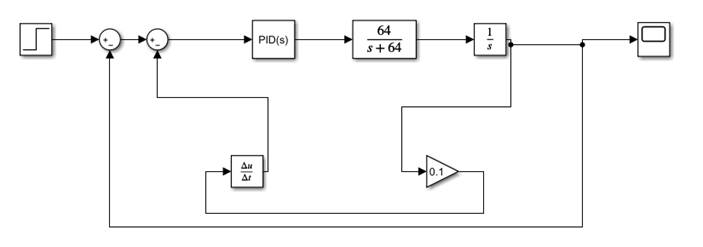
​ 图3-5 直流电机控制系统仿真图

​ 仿真后得到的阶跃响应曲线如图

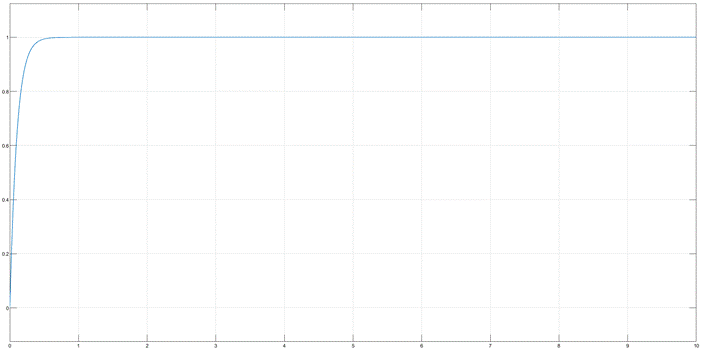
​ 图3-6 直流电机控制系统阶跃响应图

​ 系统校正前后及校正装置的Bode图如图：

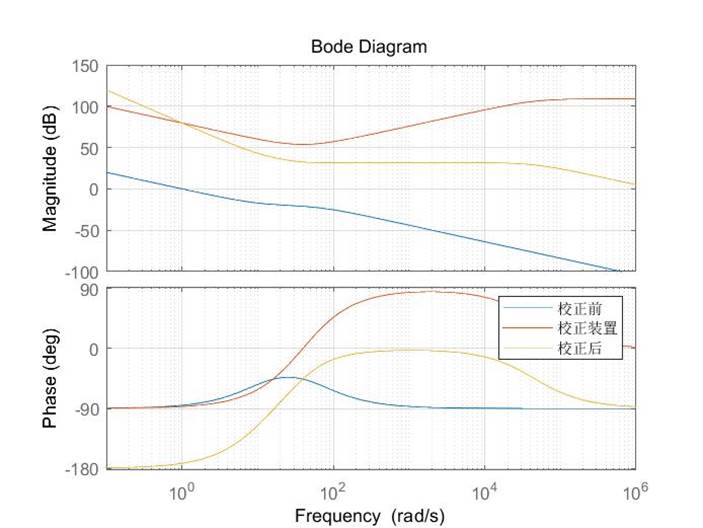
​ 图3-7 直流电机控制系统Bode图

​ 求得系统校正后超调量为4.2%，小于5%，满足要求，阶跃响应调整时间为0.0596s，小于0.6s，满足要求，且整个过程相角裕度为正，系统稳定。

代码解释

得到系统固有传递函数  

num = [6.4 64];  

den = [1,64,0];  

sys5 = tf(num,den);     

得到PID环节中积分环节的传递函数  

numi = [9615.5155];  

deni = [1 0];  

sys6= tf(numi,deni);     

得到PID环节中微分环节的传递函数  

numd = [6.1835*45167.7589,0];  *

*dend = [1 45167.7589];  *

*sys7= tf(numd,dend);     *

*得到系统校正后的开环传递函数  *

*sysz=(sys6+sys7+488.3792)*

sys5     

得到系统校正装置的传递函数  

gc=sys6+sys7+488.3792     

得到系统单位负反馈闭环传递函数  

sysjz = feedback(sysz,1)     

在图窗1绘制阶跃响应后的输出 

 figure(1)  

step(sysjz)     

在图窗2绘制校正前后及校正装置的Bode图  

figure(2)  

bode(sys5)  

hold on;  

bode(sys6+sys7+488.3792)  

bode(sysz)  

legend('校正前','校正装置','校正后')  

grid on;     

总结收获

​ 通过机器人控制原理课程设计的学习，我了解到了评价系统的一般指标及其含义，学习到了在面对一些不稳定的系统或希望具有某些要求指标的系统的校正装置的设计及仿真，具体于这两个题目，我学习到了期望特性法及PID方法，并真正实践，达到最终所要求的指标，熟练了MATLAB编程能力，也加强了手绘的能力，初步体会到了控制科学的魅力。

​ 在课程设计过程中，出现了不少问题，比如对于知识的运用不太熟悉,甚至遗忘了学过的一些内容。知其然却不知其所以然，对一些现象能观测，却不知它的原理是什么。在设计过程中也遇到了很多障碍，电路的计算、程序的编写等，都还有着很大的提升空间。在动手调整校正装置的过程中我也遇到了一些问题，比如在第二个题目中需要确定的参数较多，我们可以先固定一个参数，将其他参数调整至合适的大致范围，再调整固定的参数。