1 分析
1.1 问题简述
定义 1.1. pitch_joint : 云台俯仰运动的旋转关节(转轴),在 RoboMaster 中通常由一个 6020无刷电机作为执行器驱动。
定义 1.2. pitch_link : 连接在 pitch_joint 上的由发射机构、图传、摄像头等零件简化成的刚体,它的质量不变且质心与 pitch_joint 的距离不变。
与平衡相关的定义如下:
定义 1.3. 平衡: 通过某种方式抵消 pitch_link 带来的重力矩。
定义 1.4. 完美平衡 (Perfect Balance): 无论 pitch_joint 在什么位置角度,pitch_link 带来的重力矩都能被抵消。
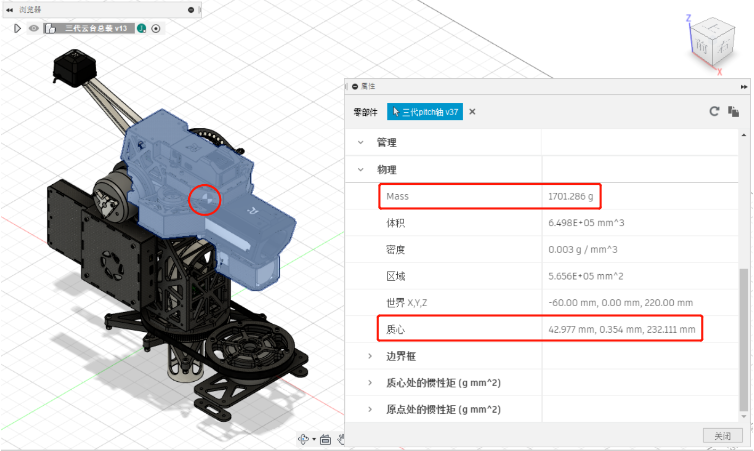
如图所示,我们队伍的英雄机器人 pitch_link 的质量为 1.701 kg,质心与 pitch_joint的距离为 0.103 m。如果没有重力补偿,使用一个 6020 电机驱动 pitch_joint 保持 pitch_link水平,电机将在两分钟内过热甚至烧毁,电控程序上使用简单的 PID 进行控制的效果不好,不满足上场比赛的性能要求。这种问题集中出现在下供弹英雄机器人和哨兵下云台上。
1.2 机构简图
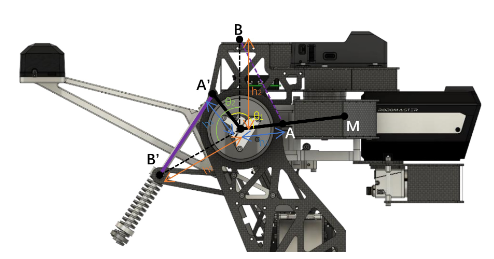
根据上述描述,有 下图中除了弹簧的部分:pitch_link 的质量为 𝑀,与 pitch_joint 的距离为 𝐿, 重力加速度为 𝑔,pitch_link 与竖直面的角度为 𝜃。
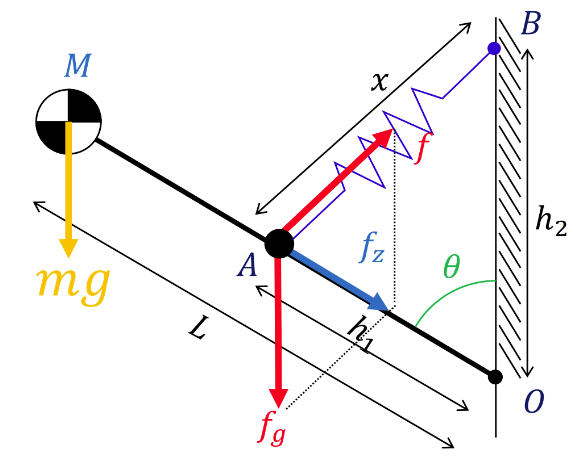
图中还有一拉簧,此拉簧为零原长弹簧,它是本文的关键,它的一段固定在 pitch_link上的 A 点,与 pitch_joint 的距离为 ℎ1 ,另一端固定在 pitch_joint 的父级 link 上(通常为yaw_link),与 pitch_joint 的距离为 ℎ2。
定义 1.5. 零原长弹簧:弹簧的两个固定端距离为 0 时拉力/推力大小为 0 ,且拉力/推力大小与两个固定端的长度成正比。
1.3 受力分析
pitch_link 所受重力作用在 pitch_joint 上的重力矩如下:
$$
𝜏 = 𝑚𝑔𝑙 sin 𝜃 (1)
$$
重力矩在 A 点的作用等价于 𝑓𝑔,如下:
$$
𝑓𝑔 = 𝑚𝑔 𝐿/h1
$$
其中 𝑘 为弹簧的劲度系数。
结合静力学可知,显然 𝑓 、 𝑓𝑧 、 𝑓𝑔 构成的力三角形与 Δ 𝐴𝑂𝐵 相似。则有
$$
𝑓𝑔/f=h2/x
$$
$$
mgL/fh1=h2/x
$$
$$
mgL/kxh1=h2/x
$$
$$
mgL/kh1=h2
$$
1.4 结论
注意到 最终式中各符号均代表常数,与 𝜃 无关,换言之:当拉簧的 𝑘 满足 下式时,图中的机构(系统)将会处于静力平衡状态。即:无论 𝜃 的值是多少,拉簧产生的拉力作用在 pitch_joint上的力矩与 pitch_link 作用在 pitch_joint 上的重力矩抵消,也就是实现了完美平衡。
$$
k=mgL/h1h2
$$
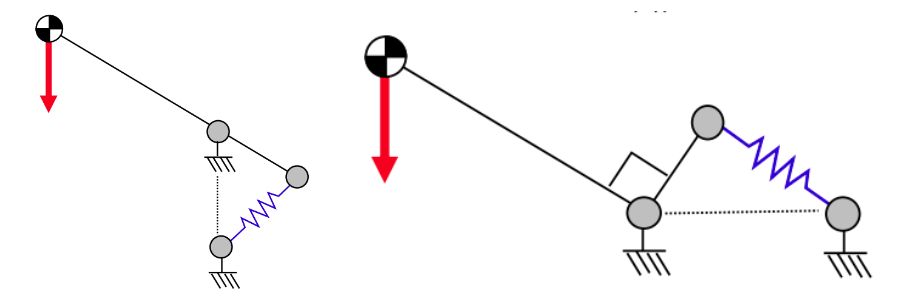
图中 A 点和 B 点可以同时绕 pitch_joint 旋转同个角角度,从而得到上述机构的等价形式,为设计带来一定自由度,可以避免和其他结构干涉。下图展示了其他两种形式。
2 实现
2.1 零原长拉簧
上述原理中已经强调,关键机构是零原长弹簧,但零原长弹簧如何实现呢–我们使用压簧和数个零件制作了零原长拉簧。如 图 4中所示:当连接点 A 与 B 间没有力的作用时,压簧完全伸展,A 与 B 重合距离为零,整个系统等价于一根完全放松时的零原长的拉簧;当连接点 A 与 B间受力分开时,当压簧压缩,A 与 B 的拉力等比于它们之间的距离,整个系统等价于一根拉伸时的零原长的拉簧。
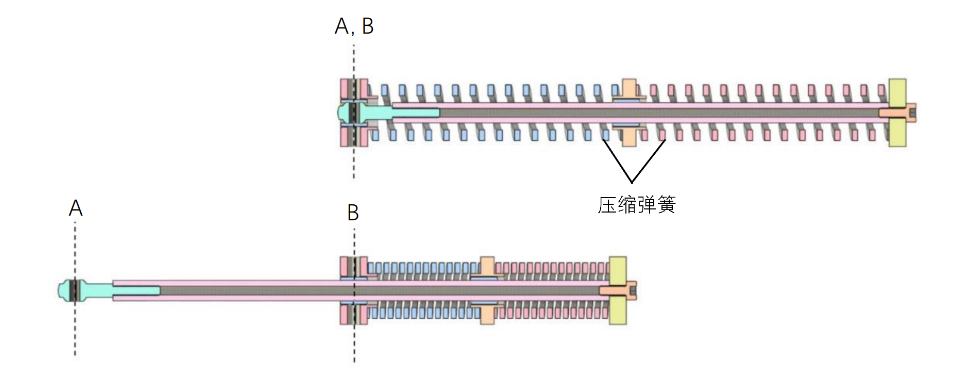
如下是设计展示。
3.参考文献
[1] HERDER J L. Energy-free systems. theory, conception and design of statically: volume 2[M]. [S.l.: s.n.], 2001.
[2] YUN S H, SEO J, YOON J, et al. 3-dof gravity compensation mechanism for robot waists with the variations of center of mass[C]//2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). [S.l.]: IEEE, 2019:3565-3570.

