Robomaster轮腿式平衡步兵设计

确定腿部杆长参数

​ 腿部五连杆机构具有两个自由度，由机架的两个关节电机提供主动力。但在本设计中，轮腿式双足机器人的腿部仅在 y 方向运动，而限制其 x 方向运动，因此两个关节电机的旋转角度同步，使五连杆机构的自由度降低至一个，故只取五连杆机构的一半进行分析， 如下图所示，图中各物理参数见下表。

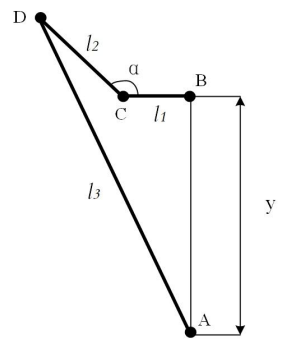
​ 列出各杆件的几何关系如下：

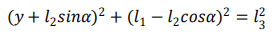
​ 整理得到高度 y 与关节转角关系如下：

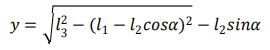
​ 下图分别是机体处于最低和最高高度时的状态

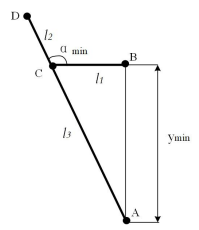
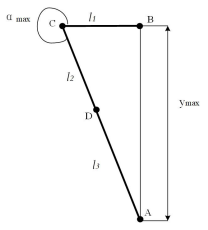
​ 由最低高度图可得到如下几何关系式

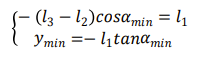
​ 由最高高度图可得到如下几何关系式

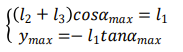
​ 联立可得到如下几何关系式：

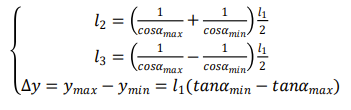
​ 可知，l2 l3 和代尔塔y均可由l1、αmax和αmin表示，故选定机架半长l1为定值，将αmax和αmin视作自变量，其约束条件如下:

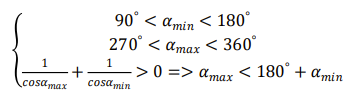
​ 根据所设计机器人参数指标，得到如下目标约束：

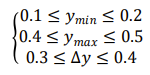
​ 为了使关节电机角度α与机体高度y尽可能呈线性关系，要求两者的相关系数：

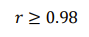
​ 用 Matlab 编写算法筛选出满足式各项约束条件的自变量值，并求出对应的杆长及ymax,ymin,\delta y

clc
clear
R=zeros(89,89);%相关系数矩阵
H=zeros(89,89);%最高高度矩阵
L=zeros(89,89);%最低高度矩阵
Y=zeros(89,89);%高度差矩阵
B=zeros(89,89);%l2杆长矩阵
C=zeros(89,89);%l3杆长矩阵
for Anglemin=91:179 %最小角度限制在90-180之间
    for Anglemax=271:359 %最大角度限制在270-360之间
        if(Anglemax>=(Anglemin+180)) %最大角度<最小角度+180
            break;
        end
        Radmin=2*pi*Anglemin/360;
        Radmax=2*pi*Anglemax/360;
        Angle=[Anglemin:1:Anglemax];
        Rad=2*pi*Angle/360;
        a=0.1; %设定l1杆的长度
        b=(a/cos(Radmax)+a/cos(Radmin))/2;
        c=(a/cos(Radmax)-a/cos(Radmin))/2;
        y=sqrt(c^2-(a-b*cos(Rad)).^2)-b*sin(Rad);%角度与高度的关系式
        R((Anglemin-90),(Anglemax-270))=min(min(corrcoef(Angle,y)));%获取角度与高度之间的相关系数
        L((Anglemin-90),(Anglemax-270))=-a*tan(Radmin);%获取最低高度
        H((Anglemin-90),(Anglemax-270))=-a*tan(Radmax);%获取最高高度
        Y((Anglemin-90),(Anglemax-270))=a*(tan(Radmin)-tan(Radmax));%获取高度差
        B((Anglemin-90),(Anglemax-270))=b;%获取l2杆长
        C((Anglemin-90),(Anglemax-270))=c;%获取l3杆长
    end
end
AngleSet=zeros(2,89);%存放筛选后角度值的矩阵
k=0;
for i=1:89
    for j=1:89
        if(R(i,j)>=0.98)%以相关系数作为筛选条件
            if((0.4<=H(i,j))&&(H(i,j)<=0.5))%以最高高度作为筛选条件
                  if((0.1<=L(i,j))&&(L(i,j)<=0.2))%以最低高度作为筛选条件
                       if((0.3<=Y(i,j))&&(Y(i,j)<=0.4))%以高度差作为筛选条件
                        k=k+1;
                        AngleSet(1,k)=i+90;%筛选后的最小角度存入矩阵
                        AngleSet(2,k)=j+270;%筛选后的最大角度存入矩阵
                       end
                  end
            end
        end
    end
end
Final=zeros(8,k);%存放筛选后的角度，以及与之对应的相关数据
for p=1:k
    Final(1,p)=AngleSet(1,p);%最小角度
    Final(2,p)=AngleSet(2,p);%最大角度
    Final(3,p)=R((Final(1,p)-90),(Final(2,p)-270));%相关系数
    Final(4,p)=H((Final(1,p)-90),(Final(2,p)-270));%最高高度
    Final(5,p)=L((Final(1,p)-90),(Final(2,p)-270));%最低高度
    Final(6,p)=Y((Final(1,p)-90),(Final(2,p)-270));%高度差
    Final(7,p)=B((Final(1,p)-90),(Final(2,p)-270));%l2杆长
    Final(8,p)=C((Final(1,p)-90),(Final(2,p)-270));%l3杆长
end
%将所有矩阵输出到excel文件中
xlswrite('E:\设计尺寸总表',R,'相关系数');
xlswrite('E:\设计尺寸总表',H,'最高高度');
xlswrite('E:\设计尺寸总表',L,'最低高度');
xlswrite('E:\设计尺寸总表',Y,'高度差');
xlswrite('E:\设计尺寸总表',B,'l2杆长');
xlswrite('E:\设计尺寸总表',C,'l3杆长');
xlswrite('E:\设计尺寸总表',Final,'筛选后数据');

​ 从中挑选出符合条件的最终参数，所对应的l2 = 0.15, l3 = 0.30 , delta y = 0.35。

平衡步兵受力分析结果

​ 平衡步兵五连杆的受力分析是五连杆控制过程中的关键部分，控制器在计算过程中需要获悉该结果并依靠该结果计算执行器预期的输出情况，同时需要该结果辅助判断机器人当前的状态。

1.需求分析

​ 我们已经大致架设好了整体的控制思路和控制框架(来自电控同学的帮助），对于已经设计好的控制器，在将数据发送给执行器之前的最后一步，控制器可以输出的内容是上层机构需求的受力情况（包括水平方向的牵引力、竖直方向的支持力和沿轴旋转的力，两侧分别能够输出这样一组参数），需要根据当前的构型得到当前情况下要让上层机构受到这样的力需要每个电机输出的扭矩，对应于平衡步兵的五连杆这里是两个关节电机和轮毂电机的输出扭矩。

​ 其次对于状态观测而言，机器人需要能够根据每个电机当前反馈的扭矩输出情况反推当前的机器人上层机构受力，因此需要重新根据电机输出扭矩的情况计算出上层机构的受力情况。

下图说明的是上层机构的受力定义，值得注意的是这里的L代表的是上层机构质心距离关节P的距离：

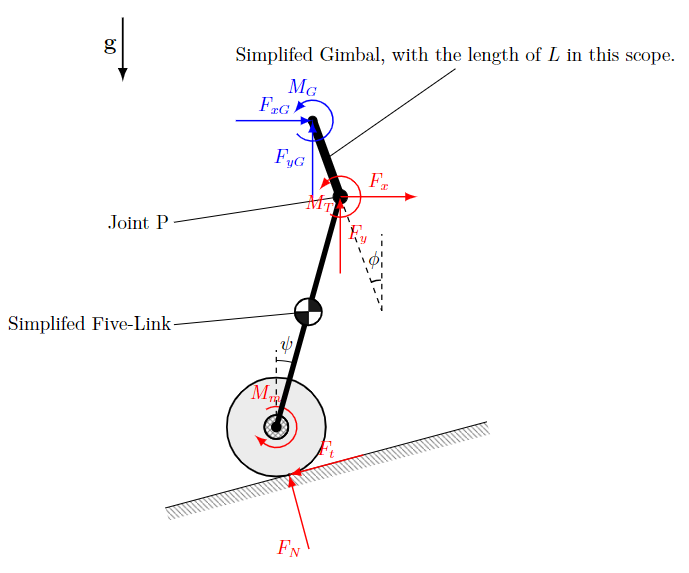
​ 机器人部分受力情况说明

下图说明的是五连杆的受力和状态定义

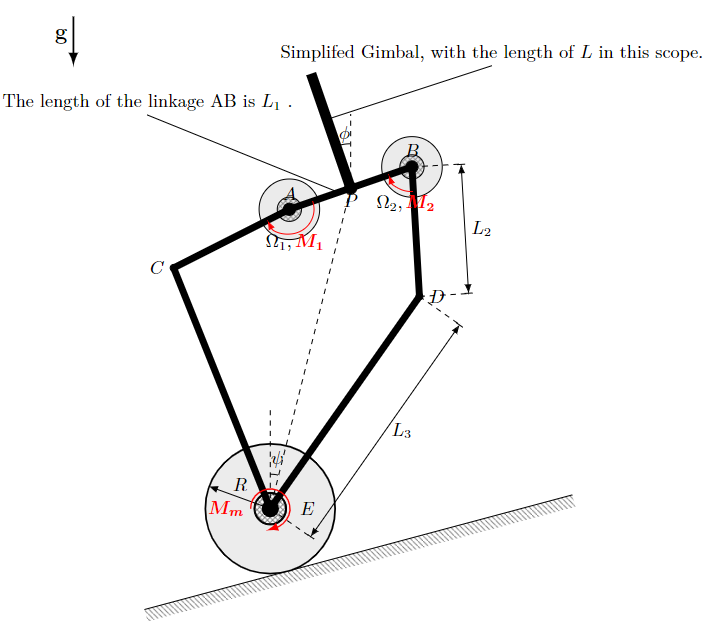
​ 部分受力情况描述，这里标注的Ω是角度，M是扭矩

这里值得注意的点就在于，在上述情况下，上层机构的实际受力情况应为用蓝色标注处的受力情况
$$
F′=(FxG,FyG,MG)T
$$
，但是考虑到实际情况中作用到上层机构的上述力系可以向关节P处简化，最终可以通过下列的数学运算等效为
$$
\textbf{F}=(F_x, F_y, M_T)^T：
\begin{cases}
F_x=F_{xG}\
F_y=F_{yG}\
M_T=M_G+F_{xG}\sin\phi+F_{yG}\cos\phi
\end{cases}
$$
因此最终在受力分析一步输入的内容可以为F向量而不是F′向量。

综上所述，控制器需要的结果应该是这样两个部分：

能够依赖当前构型Θ=(Ω1,Ω2,ψ)T计算出每一个上层机构期望受力情况向量F=(Fx,Fy,MT)T计算出当前需要每个执行器输出的扭矩向量M=(M1,M2,Mm)，即需要得到一组这样的定量表述的映射关系
$$
\displaystyle\textbf{F},\Theta\xrightarrow{f}\textbf{M}
$$
能够根据当前的执行器工作状态向量M和当前构型Θ计算出上层机构的实际受力情况辅助进行地形观测，即需要得到一组这样的定量表述的映射关系
$$
\displaystyle\textbf{M},\Theta\xrightarrow{g}\textbf{F}
$$

2.分析结果说明

电控同学给出的分析结果如下所示：

受力分析基本思路：

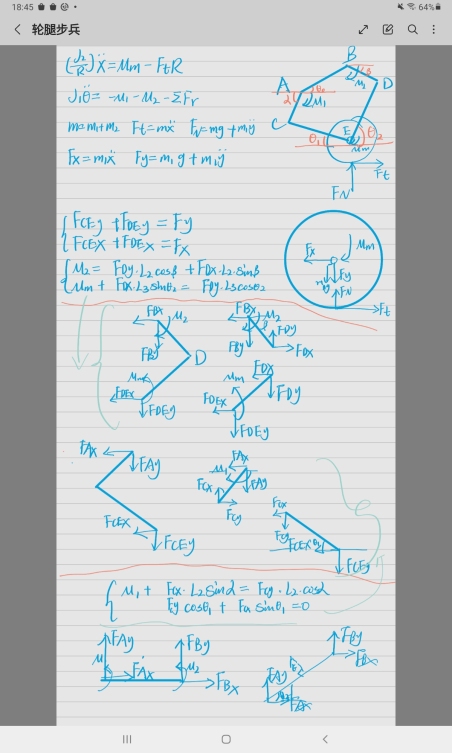
计算相关的Matlab代码：

% 已知当前的五连杆构型、关节电机输出扭矩、轮毂电机的输出扭矩
% 计算上层机构受到的沿水平和竖直方向的力和旋转的扭矩
% 加速度向右向上为正 逆时针旋转为正
clear all;
syms alpha beta theta1 theta2 M1 M2 Mm L1 L2 L3 theta0 m1 m2 g J1;%已知数据 
syms Fdex Fdey Fcex Fcey Fcy Fdy Fcx Fdx Fy Fx ddy ddx ddtheta
Leqn1=M1-(Fcx*L2*sin(alpha)-Fcy*L2*cos(alpha));
Leqn2=Fcy*cos(theta1)+Fcx*sin(theta1);
Leqn=[Leqn1 Leqn2];
[Fcx,Fcy]=solve(Leqn,Fcx,Fcy);
Reqn1=M2-(Fdx*L2*sin(beta)+Fdy*L2*cos(beta));
Reqn2=Mm-(-Fdx*L3*sin(theta2)+Fdy*L3*cos(theta2));
Reqn=[Reqn1 Reqn2];
[Fdx,Fdy]=solve(Reqn,Fdx,Fdy);
Fy=Fcy+Fdy;Fx=Fcx+Fdx;
ddy=Fy/m1-g;
ddx=Fx/m1;
ddx=simplify(ddx)
ddy=simplify(ddy)
Xa0=-L1/2;Ya0=0;Xp0=0;Yp0=0;Xb0=L1/2;Yb0=0;
%旋转矩阵
TTheta=[cos(theta0) sin(theta0) 0;-sin(theta0) cos(theta0) 0;0 0 1];
T=[Xa0 Ya0 1]*TTheta;
Xa1=T(1); Ya1=T(2);
T=[Xp0 Yp0 1]*TTheta;
Xp1=T(1); Yp1=T(2);
T=[Xb0 Yb0 1]*TTheta;
Xb1=T(1);Yb1=T(2);
ddtheta=(M1+M2+Fdy*(Xb1-Xp1)+Fcx*(Yp1-Ya1)-Fdx*(Yb1-Yp1)-Fcy*(Xp1-Xa1))/J1;
ddtheta=simplify(ddtheta)


% 输入实际的构型和实际电机输出扭矩计算上层机构的受力情况
% 这里默认轮子质量 3000kg(无穷大, 保证轮子不会发生实际转动)
% 这里默认的杆长为 [L1 L2 L3]=[0.15m 0.15m 0.3m]
Theta1=52.7903; % 连杆角度 theta1
Theta2=52.8629; % 连杆角度 theta2
Omega1=135.0478; % 关节电机角度 Omega1
Omega2=135.1716; % 关节电机角度 Omega2
M=10; % 上层机构质量
M1Real=14.9480; % M1 电机实际输出的扭矩
M2Real=15.6875; % M2 电机实际输出的扭矩
MmReal=39.6268; % Mm 电机实际输出的扭矩

% C 点受力情况计算
double(subs(Fcx,[alpha beta theta1 theta2 M1 M2 Mm L1 L2 L3 theta0 m1 m2 g],[(180-Omega1)/180*pi (180-Omega2)/180*pi Theta1/180*pi Theta2/180*pi M1Real M2Real MmReal 0.15 0.15 0.3 0 M 3000 9.8]))
double(subs(Fcy,[alpha beta theta1 theta2 M1 M2 Mm L1 L2 L3 theta0 m1 m2 g],[(180-Omega1)/180*pi (180-Omega2)/180*pi Theta1/180*pi Theta2/180*pi M1Real M2Real MmReal 0.15 0.15 0.3 0 M 3000 9.8]))
% D 点受力情况计算
double(subs(Fdx,[alpha beta theta1 theta2 M1 M2 Mm L1 L2 L3 theta0 m1 m2 g],[(180-Omega1)/180*pi (180-Omega2)/180*pi Theta1/180*pi Theta2/180*pi M1Real M2Real MmReal 0.15 0.15 0.3 0 M 3000 9.8]))
double(subs(Fdy,[alpha beta theta1 theta2 M1 M2 Mm L1 L2 L3 theta0 m1 m2 g],[(180-Omega1)/180*pi (180-Omega2)/180*pi Theta1/180*pi Theta2/180*pi M1Real M2Real MmReal 0.15 0.15 0.3 0 M 3000 9.8]))
% 上层机构受力情况计算
double(subs(ddx*m1,[alpha beta theta1 theta2 M1 M2 Mm L1 L2 L3 theta0 m1 m2 g],[(180-Omega1)/180*pi (180-Omega2)/180*pi Theta1/180*pi Theta2/180*pi M1Real M2Real MmReal 0.15 0.15 0.3 0 M 3000 9.8]))
double(subs(ddy*m1+m1*g,[alpha beta theta1 theta2 M1 M2 Mm L1 L2 L3 theta0 m1 m2 g],[(180-Omega1)/180*pi (180-Omega2)/180*pi Theta1/180*pi Theta2/180*pi M1Real M2Real MmReal 0.15 0.15 0.3 0 M 3000 9.8]))
double(subs(ddtheta*J1,[alpha beta theta1 theta2 M1 M2 Mm L1 L2 L3 theta0 m1 m2 g],[(180-Omega1)/180*pi (180-Omega2)/180*pi Theta1/180*pi Theta2/180*pi M1Real M2Real MmReal 0.15 0.15 0.3 0 M 3000 9.8]))

2.1 计算过程说明

2.1.1 符号说明

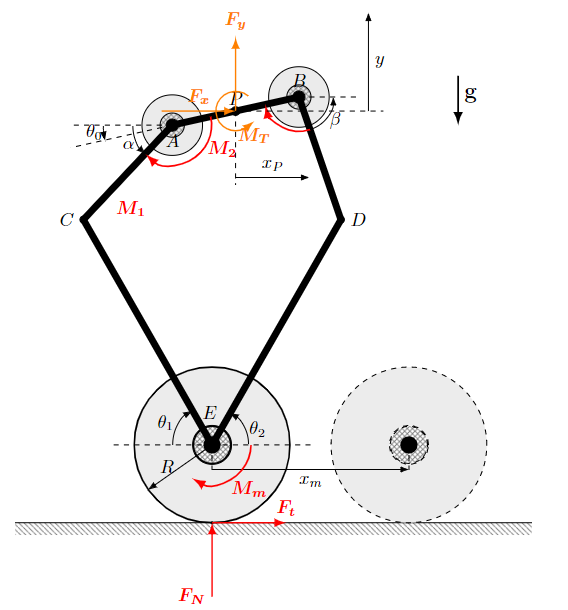
​ 受力状态参数描述

绝大多数的参数定义都参考前面的两张图片，这里对于受力分析部分定义的符号重新进行大致说明

符号	说明
J1	上层机构（包括AB杆）相对于关节P的转动惯量
J2	驱动轮毂部分的转动惯量
m1	上层机构质量
m2	驱动轮和驱动轮电机的质量
m	全车总质量
FDx	D点处ED杆对BD杆水平向右的支持力
FDy	D点处ED杆对BD杆竖直向上的支持力
FCx	C点处EC杆对AC杆水平向右的支持力
FCy	C点处EC杆对AC杆竖直向上的支持力

2.2.2 方程说明

​ 受力状态参数描述

首先第一部分，就是对于驱动轮而言，这里假定驱动轮在地面上并不发生打滑，因此可以列出驱动轮的转矩方程：
$$
J_2\frac{\ddot x_m}{R}=M_m-F_tR
$$
接下来，对于上层机构平台，可以列出这样的转动方程（注意这里的Mm是内力所以不算在这个方程里，此方程是将除了上层机构以外的所有部分全部看成整体列出来的）：
$$
M_T=J_1\ddot \theta_0=M_1+M_2+\sum_{\textrm{Joint P}}Fr
$$
这里的

Joint P∑Fr

指的是图中的Ft和FN相对于关节P的转矩，最终这些力等效于使上层机构在平面内旋转的转动扭矩MT。同时由于图中画的M1和M2都是电机输出的扭矩，作用到AB杆上就是他们的反作用力，因此在式子中均为正号。

当然下面这几个方程也是从整体-隔离法就可以显然得到的：
$$
\begin{cases}
m=m_1+m_2\
F_t=m_1\ddot x_P+m_2\ddot x_m\
F_N=mg+m_1\ddot y\
F_x=m_1\ddot x_P\
F_y=m_1(g+\ddot y)
\end{cases}
$$
单独对AB杆受力分析就可以得到这样的方程：
$$
\begin{cases}
F_x=F_{CEx}+F_{DEx}\
F_y=F_{CEy}+F_{DEy}
\end{cases}
$$
分别将BD杆和DE杆的受力向B点和E点简化（见图中的受力分析），列扭矩方程可得：
$$
\begin{cases}
\begin{align}
B点：M_2&=+F_{Dx}L_2\sin\beta+F_{Dy}L_2\cos\beta\
E点：
M_m&=-F_{Dx}L_3\sin\theta_2+F_{Dy}L_3\cos\theta_2
\end{align}
\end{cases}
$$
同理A点处有：
$$
M_1=F_{Cx}L_2\sin\alpha-F_{Cy}L_2\cos\alpha
$$
最后就是EC杆是二力杆的条件：
$$
F_{Cx}\sin\theta_1+F_{Cy}\cos\theta_1=0
$$
到这里并不难发现，上述的受力分析做出的假设有这么几点：

五连杆机构内存在质量和转动惯量的部分只有AB杆（包括上层云台）和轮毂；轮毂电机固定在DE杆上，CE杆两端都是轴承因而为二力杆。

最后就是可以通过C、D两点的受力参数计算出关节P处受到的力学参数：

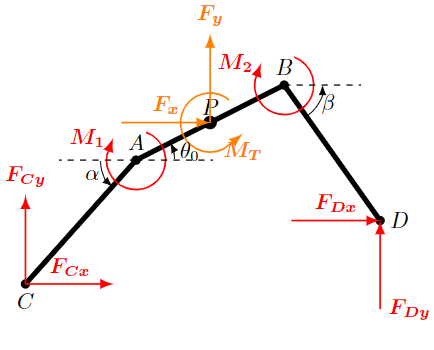
$$
⎧Fx​=FCx​+FDx
Fy​=FCy​+FDy
⎨MT​=M1​+M2​+(FCx​−FDx​)2L1​​sinθ0​−(FCy​−FDy​)2L1​​cosθ0
$$
最后扭矩这一行的式子需要注意这里不能直接把CABD杆看成一个整体，因为这个力偶总共会让三根杆发生转动，而我们只想要使AB杆转动的一部分，这里可以把C点和D点受到的力平移到A点和B点。

2.2.3 程序说明

这是一个Matlab的实时脚本，主要存在两个节，这里分别对两个部分进行阐述说明，不过如果对于这一部分并不感兴趣的话也可以跳过下面的这两部分。

2.2.3.1 第一部分程序

第一部分的程序主要是在完成需求分析里
$$
\displaystyle\textbf{M},\Theta\xrightarrow{g}\textbf{F}
$$
的映射，这里面最终输出的变量ddx就是
$$
\frac{F_x}{m_1}
$$
，ddy就是
$$
\frac{F_y}{m_1}
$$
，

ddtheta

就是
$$
\frac{M_T}{J_1}
$$
，而程序中的H可以定义为上文中给出的上层机构质心到关节P的距离L，为了获得上述需求的MT这里可以将H写为0。这里的主要求解思路就是分别先通过A点处列出的扭矩平衡方程 和 EC杆为二力杆的条件与B点处列出的扭矩平衡方程 和 E点处的扭矩平衡方程

使用已知条件分别计算出C点和D点传递的力，通过C点和D点传递的力可以结出最终关节P传递的力学参数结果为：
$$
\begin{cases}
\begin{align}
F_x&=\frac{M_1 \cos\theta_1}{L_2 \sin(\alpha +\theta_1 )}-\frac{L_2 M_m\cos\beta-L_3 M_2 \cos\theta_2}{L_2 L_3 \sin(\beta +\theta_2 )}\
&=\frac{\cos\theta_1}{L_2 \sin(\alpha +\theta_1 )}M_1+\frac{\cos\theta_2}{L_2\sin(\beta +\theta_2 )}M_2+\frac{-\cos\beta}{L_3 \sin(\beta +\theta_2 )}M_m\
F_y&=\frac{L_2 M_m\sin(\alpha +\theta_1 )\sin\beta +L_3 M_2 \sin(\alpha +\theta_1 )\sin\theta_2 -L_3 M_1 \sin(\beta +\theta_2 )\sin\theta_1 }{L_2 L_3 \sin(\alpha +\theta_1 )\sin(\beta +\theta_2 )}\
&=\frac{-\sin(\beta +\theta_2 )\sin\theta_1 }{L_2\sin(\alpha +\theta_1 )\sin(\beta +\theta_2 )}M_1+\frac{\sin(\alpha +\theta_1 )\sin\theta_2}{L_2\sin(\alpha +\theta_1 )\sin(\beta +\theta_2 )}M_2+\frac{\sin(\alpha +\theta_1 )\sin\beta}{L_3 \sin(\alpha +\theta_1 )\sin(\beta +\theta_2 )}M_m\
M_T&= M_1 +M_2 +\frac{L_1 M_1 \sin(\theta_0 +\theta_1 )}{2L_2 \sin(\alpha +\theta_1 )}+\frac{L_1 \sin\theta_0{(L_2 M_m\cos\beta-L_3 M_2 \cos\theta_2 )}}{2L_2 L_3 \sin(\beta +\theta_2 )}+\frac{L_1 \cos\theta_0{(L_2 M_m\sin\beta+L_3 M_2 \sin\theta_2)}}{2L_2 L_3 \sin(\beta +\theta_2 )}\
&=\frac{2L_2 \sin(\alpha +\theta_1 )+L_1 \sin(\theta_0 +\theta_1 )}{2L_2 \sin(\alpha +\theta_1 )}M_1+\frac{2L_2 \sin(\beta +\theta_2 )-L_1 \sin(\theta_0 -\theta_2 )}{2L_2 \sin(\beta +\theta_2 )}M_2+\frac{L_1 \sin(\beta +\theta_0 )}{2L_3 \sin(\beta +\theta_2 )}M_m
\end{align}
\end{cases}
$$

2.2.3.2 第二部分程序

第一部分程序经分析已经完成了
$$
\displaystyle\textbf{M},\Theta\xrightarrow{g}\textbf{F}
$$
的映射关系，那么第二部分显然就是在完成
$$
\displaystyle\textbf{F},\Theta\xrightarrow{f}\textbf{M}
$$
的映射关系，还是来看这里的总体计算思路。

确认已知参数为当前需要的上层机构力学状态，于是首先给出方程为上层机构的受力表达式即将上层机构状态转化到CD两点的受力情况上，接下来可列写CD两点的受力情况约束得到这两点的受力表达式，最终将表达式回代即可得到下面的结果：
$$
\begin{cases}
\begin{align}
M_1&=-\frac{2L_2 \sin(\alpha +\theta_1 ){(2F_yL_2 \cos\beta -2M_T+2F_xL_2 \sin\beta +F_yL_1 \cos\theta_0 -F_xL_1 \sin\theta_0 )}}{4L_2 \sin(\alpha +\theta_1 )+4L_1 \sin(\theta_0 +\theta_1 )-4L_2 \sin(\beta -\theta_1 )}\
&=-\frac{L_2 \sin(\alpha +\theta_1 ){(2L_2 \sin\beta-L_1 \sin\theta_0)}}{2L_2 \sin(\alpha +\theta_1 )+2L_1 \sin(\theta_0 +\theta_1 )-2L_2 \sin(\beta -\theta_1 )}F_x\
&\quad-\frac{L_2 \sin(\alpha +\theta_1 ){(2L_2 \cos\beta +L_1 \cos\theta_0)}}{2L_2 \sin(\alpha +\theta_1 )+2L_1 \sin(\theta_0 +\theta_1 )-2L_2 \sin(\beta -\theta_1 )}F_y\
&\quad+\frac{L_2 \sin(\alpha +\theta_1 )}{L_2 \sin(\alpha +\theta_1 )+L_1 \sin(\theta_0 +\theta_1 )-L_2 \sin(\beta -\theta_1 )}M_T\
M_2&=\frac{2L_2 {(2M_T\cos\beta\sin\theta_1-2M_T\sin\beta\cos\theta_1+2F_yL_2 \cos\alpha\cos\beta\sin\theta_1+2F_yL_2 \cos\beta\sin\alpha\cos\theta_1+2F_xL_2 \cos\alpha\sin\beta\sin\theta_1+2F_xL_2 \sin\alpha\sin\beta\cos\theta_1+F_yL_1 \cos\beta\cos\theta_0\sin\theta_1+2F_yL_1 \cos\beta\cos\theta_1\sin\theta_0+F_yL_1 \sin\beta\cos\theta_0\cos\theta_1+F_xL_1 \cos\beta\sin\theta_0\sin\theta_1+2F_xL_1 \sin\beta\cos\theta_0\sin\theta_1+F_xL_1 \sin\beta\cos\theta_1\sin\theta_0)}}{4L_2 \sin(\alpha +\theta_1)+4L_1 \sin(\theta_0 +\theta_1)-4L_2 \sin(\beta -\theta_1)}\
&=\frac{L_1L_2(\sin\theta_1\sin(\beta+\theta_0)+\sin\beta\sin(\theta_0+\theta_1))+2L_2^2\sin\beta\sin(\alpha+\theta_1)}{2L_2 \sin(\alpha +\theta_1)+2L_1 \sin(\theta_0 +\theta_1)-2L_2 \sin(\beta -\theta_1)}F_x\
&\quad \ +\frac{L_1L_2(\cos\theta_1\sin(\beta+\theta_0)+\cos\beta\sin(\theta_0+\theta_1))+2L_2^2\cos\beta\sin(\alpha+\theta_1)}{2L_2 \sin(\alpha +\theta_1)+2L_1 \sin(\theta_0 +\theta_1)-2L_2 \sin(\beta -\theta_1)}F_y\
&\quad \ -\frac{L_2 \sin(\beta -\theta_1 )}{L_2 \sin(\alpha +\theta_1 )+L_1 \sin(\theta_0 +\theta_1 )-L_2 \sin(\beta -\theta_1 )}M_T\
M_m&=\frac{L_3 \cos\theta_2{(2M_T\sin\theta_1+2F_yL_2 \cos\alpha\sin\theta_1+2F_yL_2 \sin\alpha\cos\theta_1-2F_yL_2 \sin\beta\cos\theta_1-2F_xL_2 \sin\beta\sin\theta_1+F_yL_1 \cos\theta_0\sin\theta_1+2F_yL_1 \cos\theta_1\sin\theta_0+F_xL_1 \sin\theta_0\sin\theta_1)}}{2{(L_2 \sin(\alpha +\theta_1 )+L_1 \sin(\theta_0 +\theta_1 )-L_2 \sin(\beta -\theta_1 ))} }-\frac{L_3 \sin\theta_2{(2F_yL_2 \cos\beta\cos\theta_1-2M_T\cos\theta_1+2F_xL_2 \cos\alpha\sin\theta_1+2F_xL_2 \sin\alpha\cos\theta_1+2F_xL_2 \cos\beta\sin\theta_1+F_yL_1 \cos\theta_0\cos\theta_1+2F_xL_1 \cos\theta_0\sin\theta_1+F_xL_1 \cos\theta_1\sin\theta_0)}}{2{(L_2 \sin(\alpha +\theta_1 )+L_1 \sin(\theta_0 +\theta_1 )-L_2 \sin(\beta -\theta_1 ))} }\
&=-\frac{L_1L_3(\sin\theta_0\sin(\theta_2-\theta_1)+\sin\theta_2\sin(\theta_0+\theta_1))+2L_2L_3(\sin\theta_1\sin(\beta+\theta_2)+\sin\theta_2\sin(\alpha+\theta_1))}{2L_2 \sin(\alpha +\theta_1 )+2L_1 \sin(\theta_0 +\theta_1 )-2L_2 \sin(\beta -\theta_1 )}F_x\
&\quad-\frac{L_1L_3(\cos\theta_1\sin(\theta_2-\theta_0)-\cos\theta_2\sin(\theta_0+\theta_1))+2L_2L_3(\cos\theta_1\sin(\beta+\theta_2)-\cos\theta_2\sin(\alpha+\theta_1))}{2L_2 \sin(\alpha +\theta_1 )+2L_1 \sin(\theta_0 +\theta_1 )-2L_2 \sin(\beta -\theta_1 )}F_y\
&\quad+\frac{L_3 \sin(\theta_1 +\theta_2 )}{L_2 \sin(\alpha +\theta_1 )+L_1 \sin(\theta_0 +\theta_1 )-L_2 \sin(\beta -\theta_1 )}M_T\
\end{align}
\end{cases}
$$

2.2.4 计算结果分析

​ 首先，可以说明的是通过上述计算确实是可以给出我们想要的受力分析结果的，但是肉眼可见的就是上述计算的计算量非常地大，以致于单片机应该是够呛能够在控制过程中计算完成的。因此需要来分析上述结果以尝试进行化简来降低算力需求。

2.2.4.1.1 验证性仿真思路

​ 从上述原本的计算结果不难想到，该换算的重要中间变量其实主要在于C点和D点处的轴承的约束力，这两点处的约束力构建了受力情况向量F与执行器输出的扭矩向量M之间的桥梁。仿真的搭建其实可以考虑为平衡步兵的等效模型，这里选用的等效模型是使用钉子和胶水等思维物体效地简化平衡步兵整体来实现简化思考的效果。

​ 首先介绍这里的模型思路。考虑这样一件事情，实际上五连杆通过关节传递到上层机构的就是两个东西：力和力偶。这里的力偶就直接等于关节电机的输出扭矩，这是直接可以知道的，最后剩下的就是力的传递了。

​ 这样，我们就考虑将这里的五连杆受力使用纯受力的方式来描述，考虑方式为，在原有的五连杆构型确定的基础上，在A和B两点钉上钉子使之不能相对于当前构型发生变化，然后在轮子的触地点粘上足够强力胶水使轮子不能发生转动，于是在构型确定的基础上，对于任意的电机的输出扭矩，A和B点钉子的受力就可以直接反映上层机构的受力情况。于是此部分相当于是对于从C、D两点的受力参数到执行器输出的扭矩向量M之间的转换验证。

​ 接下来就开始搭建上述钉子-五连杆-胶水模型，首先，可以通过大地坐标系下的二维平动铰链定义A和B点，由于铰链可以指定固定的关节位置同时设置为传感当前关节的受力（实际表述为关节受力自动计算），这里的两个钉子就设置为手动指定相对于大地坐标系的坐标，然后传感两个方向上的受力，通过旋转铰链作为关节电机指定电机输出扭矩时自动计算姿态，最后就是主要要把轮毂电机固定在一个固定的杆上带动一个轮子的辐条（这里暂时不知要该怎么把轮子粘在地上所以这里选择把一个轮子中的长方体辐条固定在大地上）。

最终的模型就是这样子：

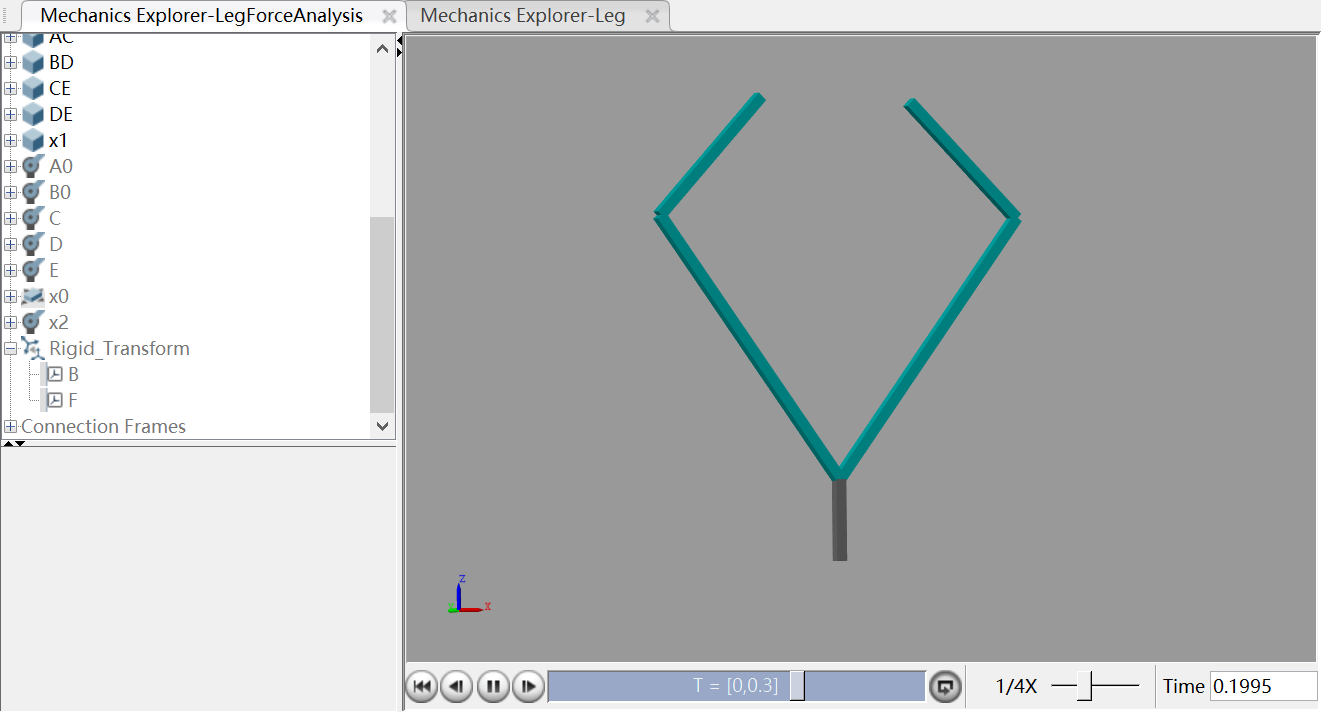
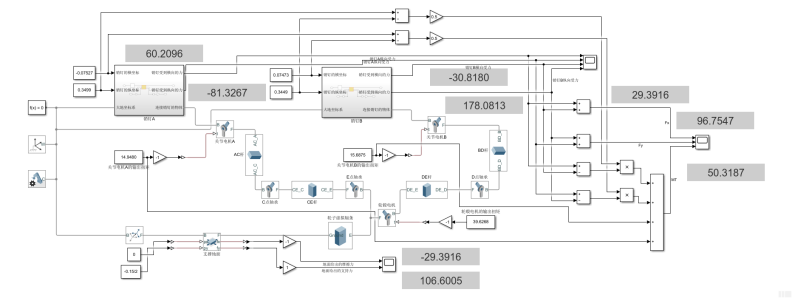
仿真文件放在这里：

2.2.4.1.2 验证流程和结果

​ 主要思路就是从程序中指定一个固定的参数，然后通过程序计算出一套需求的电机输出扭矩，然后根据电机的输出扭矩带入仿真中得到最终上层机构的受力参数，与原本在程序中预先设置的参数进行比较就可以得到计算结果的正确性。

​ 这里需要的中间过程就是，原始matlab计算文件中指定的内容是角度数据，而仿真中需要指定的构型参数是坐标数据，这两者相对应起来需要使用几何计算工具，这里使用的是geogebra在线版搭建五连杆构型并获得几何参数输入到两者中：

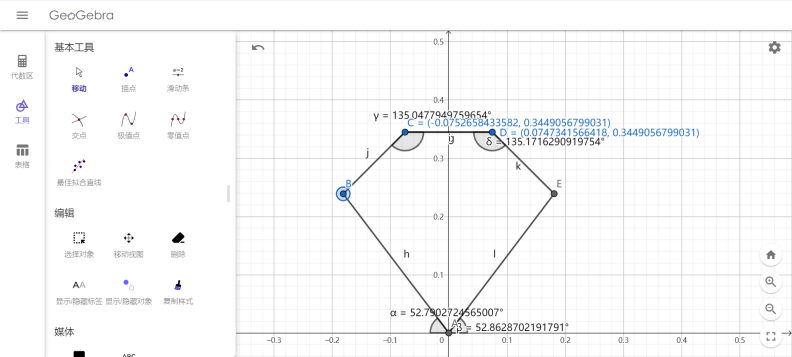
这样，就可以输入计算文件参数为：

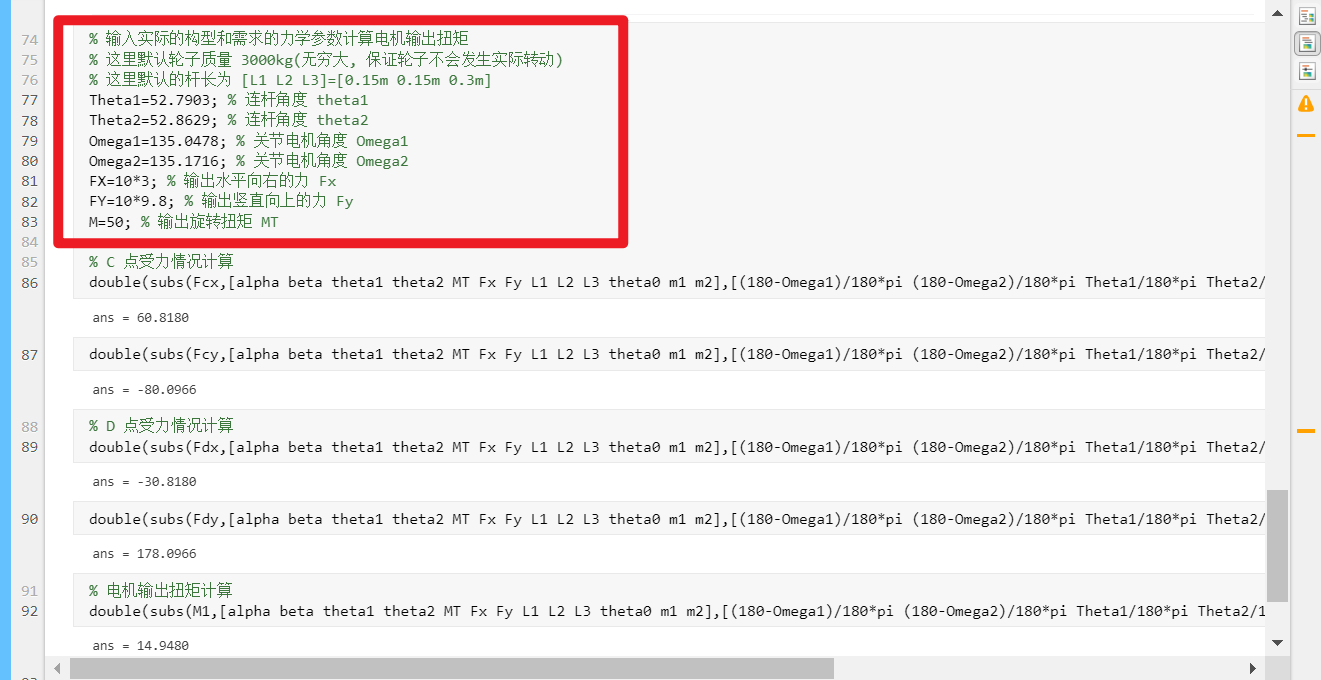
最终输出结果为：

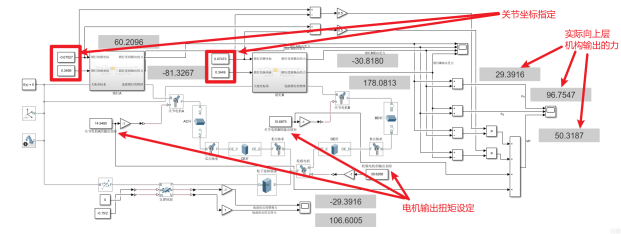
​ 如前所述，这里仿真只负责计算出钉子受到的力，最后一步的受力转化还是需要手动进行，不过也可以从仿真中验证钉子受到的力和理论计算也是一致的。应当说上述计算结果是没有出现问题的。至少这一步应该可以是被证明正确的。

3.总结

​ 最终，本受力分析给出的结果是，在于这样的参数假定情况下，执行器输出的扭矩向量M=(M1,M2,Mm)T与上层机构期望受力情况向量F=(Fx,Fy,MT)T之间的转换关系。

​ 受力状态参数描述

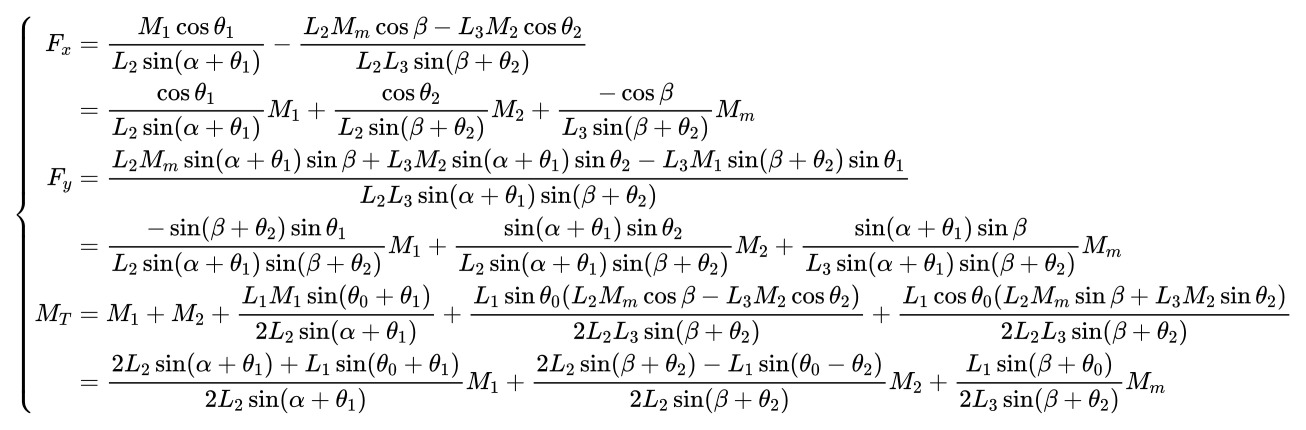
这是需求中的逆运算，而其正运算则为上述矩阵的逆，最终结果为：

轮腿步兵电机选型文档

对轮腿步兵的电机需求进行计算，以辅助进行电机的相关选型。

0.轮腿步兵参数假定

​ 进行关节电机的受力分析时上层机构近似认为是质量均匀分布的板状或均匀分布的两条棒状物体，并假定上层机构总重量为18kg；在下图中，假定l1=l2=150mm,l3=300mm，其中长度为l1的杆代表上层机构，相关假设可见假设1，长度为l2的杆质量均匀，每根的质量均为0.8kg，长度为l3的质量均匀杆的杆重为1kg；机器人上暂时不考虑其他有质量物体，故机器人总重为25.2kg；

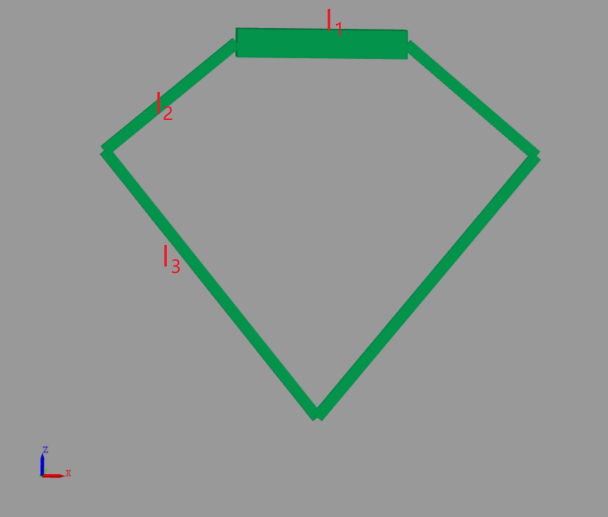
平衡步兵左右两腿间距假定为L=0.6m；

​ 下图为平衡步兵上电以后默认工作的状态，关节电机固定在图中标注红圈的位置，关节电机角度为如图所定义方向，其中此状态下关节电机的关节角度为200°；

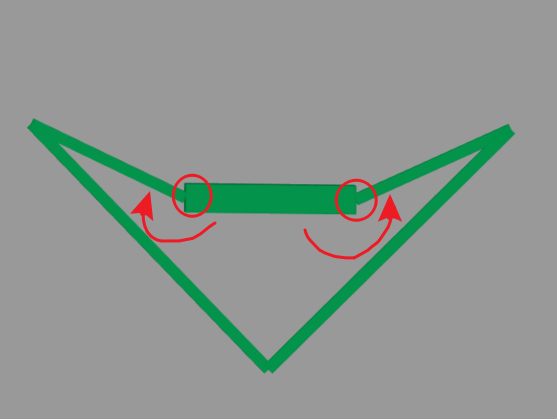
轮腿步兵的动力轮半径选择为不大于r=10cm；

假定进行关节电机的受力分析时不需要考虑轮毂动力轮对连杆机构的力偶。

1.关节电机选型分析

1.关节电机受力计算

​ 本部分主要用于进行五连杆轮腿步兵的简单受力仿真，主要是用于进行简单的受力分析以便辅助进行相关电机的选型，实际上无法通过文档中的仿真方法给出各个构型下实际关节的受力表达式。文档中使用的工具是Simulink中的机械仿真相关的内容，为考虑了五连杆上层机构质量、杆重和轮毂处的摩擦力的静态力学结构。

1.建模思路

​ 本仿真建立的基础是在于现行的基础结构，也就是轮腿结构部分采用平面五边形结构，而提及关节电机的固定位置，如果关节电机的固定在轮腿部分的中间，传动上可能会存在比较大的机械制作难度，而且暂时也没有分析得到比较明显的优势，目前比较成熟的方案也是固定上层机构上的结构，所以选定电机固定位置是将电机固定在上层机构上。

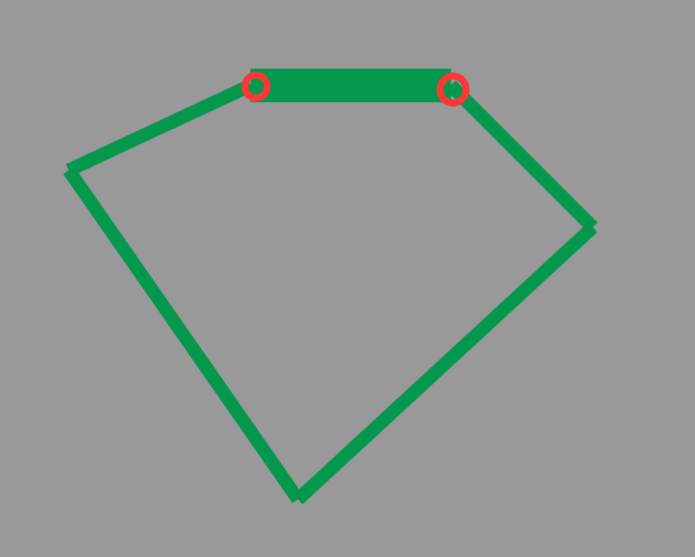
关节电机固定在上层机构的情况

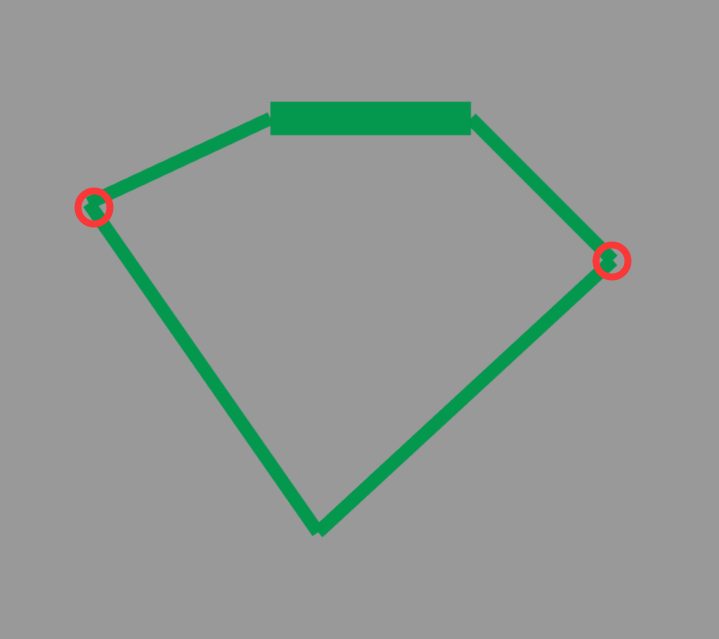
关节电机固定在轮腿中间的情况

​ 由于轮腿结构的随机器人左右两侧是对称的，这里只考虑机器人一侧的轮腿情况，此时在轮腿五边形内考虑受力情况，这里将上层机构简化为质量均匀的方块，在方块两端分别通过旋转铰链连接了对应杆长的关节杆构成平面五边形。但是为了保证平衡步兵在保持直立的情况下受力仿真的正确运行，此处做了以下等价的变换：

​ 由于轮腿步兵能够站立的关键一环是轮毂电机的作用，而此仿真并没有考虑轮毂电机与地面的摩擦力情况，但是考虑到此摩擦力可以由地面直接作用，我们考虑将五边形的最下方节点通过旋转铰链直接固定在地面上，即只进行静态受力仿真而不进行动态仿真；

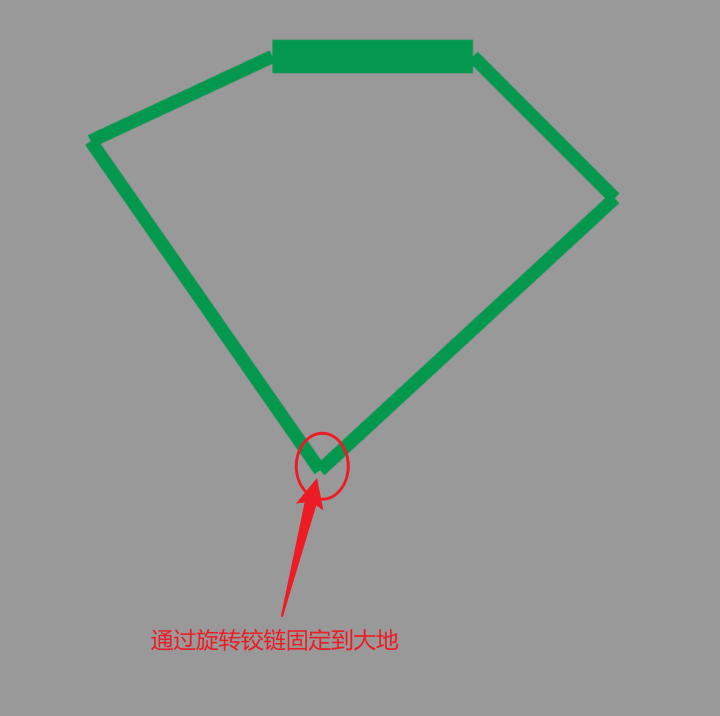
​ 为了保证平衡步兵车体的平衡姿态，这里讲上层机构通过该平面内的水平和竖直移动铰链和旋转铰链固定到地面上，但是由于需要限制上层机构的水平状态，这里通过一组虚拟的PID控制器限制了旋转铰链和水平移动铰链之间的约束关系，即需要通过水平移动铰链提供约束力使得旋转铰链不需要输出扭矩。这一步骤对应到实际系统中可以理解为机器人通过惯性力抵消了自身的转动倾向，这是合理且符合物理规律的。

​ 为了能够保持对应的构型并能够得到对应关节电机的输出扭矩，这里我们将关节电机所在的旋转铰链限制为固定角度，相当于内置角度闭环，同时反馈对应关节的输出扭矩作为观测到该点承受的扭矩。

最终建立了如下的模型：

2.受力仿真结果分析

​ 要想分析出各种工作状态下的最大输出扭矩，当前最简单的想法就是将各种平衡状态下的工作扭矩计算出来，然后考虑加速状态下的工况，由此计算出相关的需求扭矩。

1.静态受力分析

​ 首先考虑步兵整体静止的情况下的受力分析情况，此时只有一个因变量，也就是关节角度，这里考虑在可行域内对角度进行一部分的遍历得到一条大致的姿态-扭矩变化曲线：

关节角度225°，此时输出扭矩为0.53Nm

关节角度142°，此时输出扭矩为10.1Nm

关节角度90°，此时输出扭矩为2.2Nm

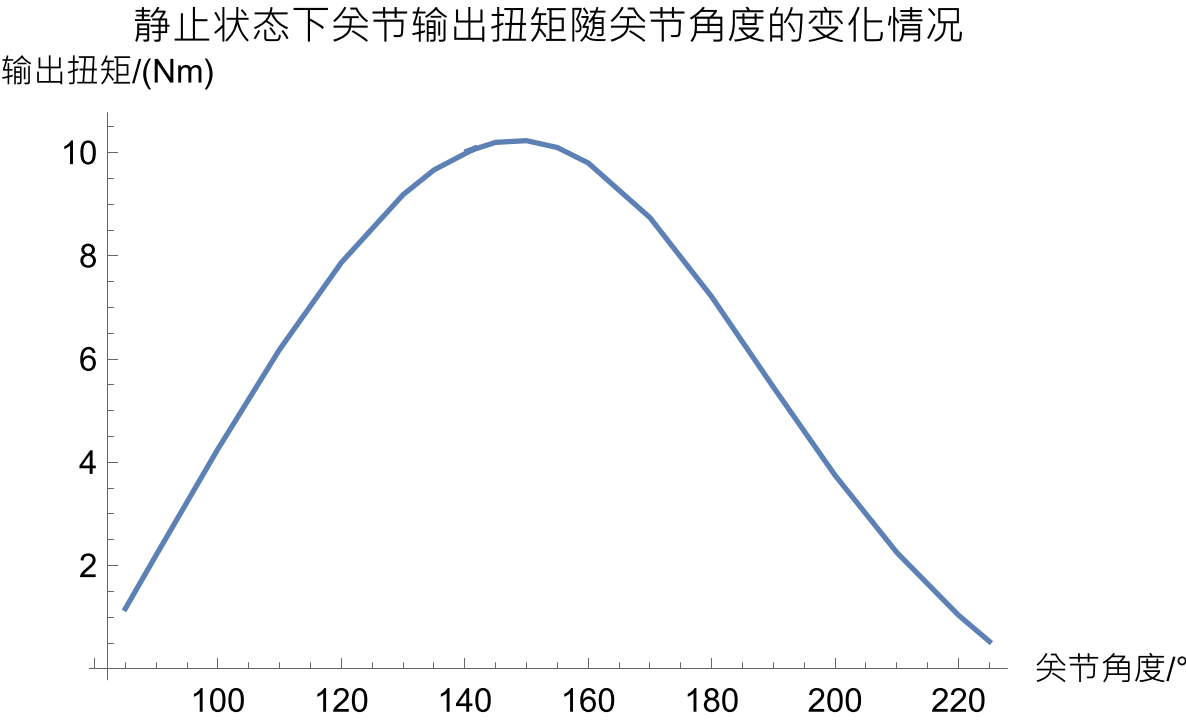
​ 此过程中发现关节角度大约在关节角度145°左右时取到极值约10.3Nm。同时还发现一个事实，也就是在上述条件下从最低点运动到最高点的上层机构行程大约30cm。

​ 同时，为了模拟机器人上层机构需要竖直向上加速的情况，我们可以将上层机构的质量增大80%到达32kg重新计算可以得到此时最大的关节电机扭矩大约17Nm。

2.加速状态受力分析

​ 在上述的10.3Nm的情况下开始考虑水平方向的加速度可得如下情况，首先我们考虑水平加速度的产生，在轮腿倾斜时，对轮腿步兵受力分析可得水平方向地面摩擦力与惯性力构成的力偶大致和重力与支持力构成的力偶平衡，因此在上层机构质心高度保持不变是水平加速度与质心和末端轮毂之间的水平距离成正比。例如在下述情况下，已测得上层机构质心相对轮毂偏移距离为l，上层机构重心高度为h，则可知：

重力与整车的支持力产生的力偶近似等于MG=mgl，而摩擦力与惯性力产生的力偶等于Mf=fh=mah，上述两力偶相等时方可保证机器人在当前状态下受力稳定，所以可以得到加速度近似为a=hgl.显然在上层云台处于不同高度的情况下受集合关系约束都存在最大的水平移动距离，该几何关系暂时可以考虑为，最上层五边形想要在某一高度上尽可能向右运动，那么该运动的极限状态就是右侧两连杆攻陷，此时右侧电机的关节角度可以计算为θ1=arctanl2+l3h，其中l2和l3分别代表两根连杆的长度。而左侧关节电机的角度可以通过分别解两次三角形来获得，表达式比较复杂，这里暂时不做描述。

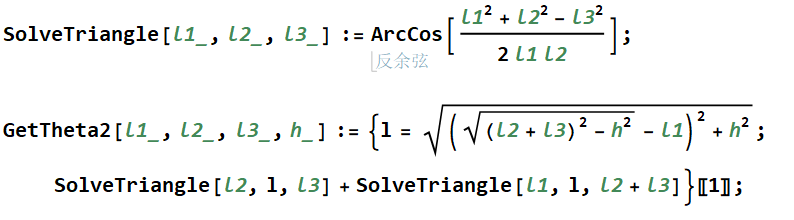
​ 通过上述表达式可以计算出另一侧关节电机的对应角度，最终可以在不同高度下对于机器人能够在水平方向产生最大加速度的情况做受力分析，得到如下结果：

最大加速度2.36g

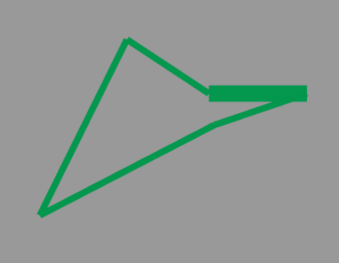
最大加速度1.82g

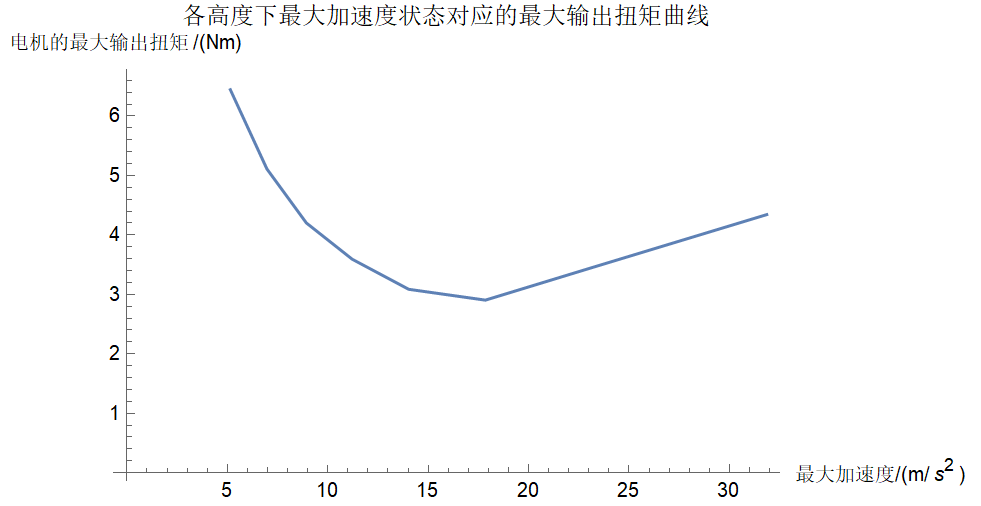
​ 可见其实最大加速度情况下电机需要输出的扭矩并不是很大，主要的加速状态下的输出扭矩可能都由平衡状态的基数提供，于是可以考虑在平衡状态下最大输出扭矩附近进行同高度的加速度计算，故需要重新进行数学公式计算，需要计算在上层机构高度保持不变时运动过程中需要两个关节电机保持的角度满足的关系：

​ 在高度已知的情况下，只需要解三个三角形即可得出对应的关节角度：

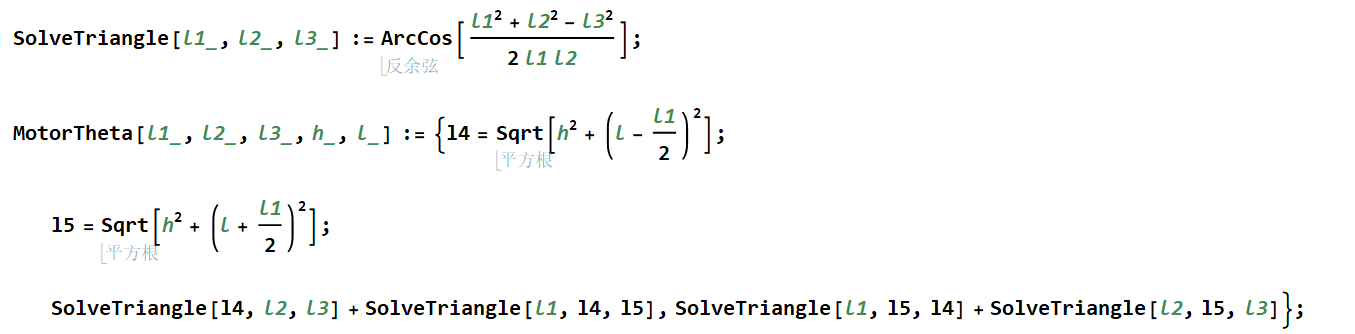
​ 选定静态受力分析时最大的约142°时的关节角度计算可得此时的上层机构高度为0.3184m，保持此高度逐渐增加水平加速度可得此过程中电机输出扭矩随姿态的变化：

高度0.3184m，水平加速度0.188g情况下，最大扭矩10.6466Nm

​ 不难发现此过程中电机需要输出的最大扭矩大约为11Nm，此时如果再考虑上层云台需要竖直向上0.8g的加速度，重新计算可得此状态下的最大电机输出扭矩为18Nm。

3.关节电机扭矩需求小结

​ 通过简单计算可以发现，如果不考虑竖直方向的加速度需求，平衡步兵工作时轮腿关节电机为保持姿态最大只需要约11Nm的输出扭矩，而且此过程可以产生1g的水平加速度，但是如果想要此过程中产生竖直向上0.8g的加速度，就可能需要使用到18Nm的输出扭矩。如果在此过程中需要重新考虑控制器的控制余量，那么就需要在原有扭矩基础上为控制器预留20%的余量，最终结果就是：

是否需要平衡步兵跳跃 需要关节电机的扭矩

22Nm 14Nm

2.关节电机转速计算

​ 正常状态下在带有控制器的情况下实际并不希望关节电机产生转动，所以实际计算过程中的关节电机需要的转速应该考虑以下两种情况：

1. 关节电机控制姿态起到主动悬挂的效果；
2. 关节电机在控制姿态改变过程中的阶跃响应速度需求。

现在分别考虑两种情况：

1.主动悬挂需求

​ 假设轮腿步兵整体可以做到6m/s的平移速度，那么对于主动悬挂需求最高的起伏路段来说，起伏路段上的突起对车体造成的影响主要是车体会存在Roll轴上的扰动需要五连杆机构来平衡。

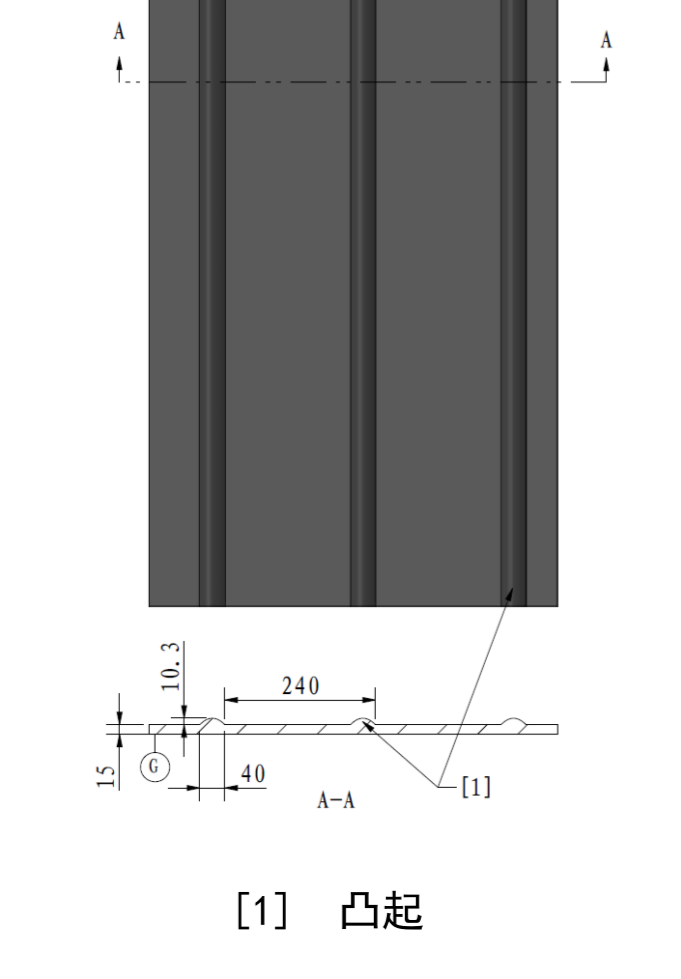
​ 参照规则上提出的起伏路段参数，假定控制器可以控制五连杆为不可旋转的理想刚体可以得到路面上的每一个突起长度都会对车体造成周期近似为T1=5m/s40mm×2=16ms，幅值近似为A1=arctan0.5m10.3mm≈0.5m10.3mm=0.0206rad的正弦扰动，该扰动的频率为f1=T11=62.5Hz，而角速度扰动幅值为A1ω=ω1A1=T12πA1=8.089rad/s=463.5∘/s，在此情况下，如果电机的执行带宽能够到达200Hz，控制器和执行器带宽近似可以容忍该频率的扰动，在精心设计控制器的情况下理论上可以使得被控对象免受该频率的干扰的控制效果，在该情况下需要电机在满足平衡状态需求的情况保持A1ω的输出转速，该转速实际值为78rpm。

2.姿态改变时阶跃响应需求

​ 在轮腿步兵的大部分工况下，需要关节电机快速响应的场合一般只存在于姿态的改变上尤其是加减速时的水平方向上快速移动整车重心，现假设轮腿步兵从默认的初始状态开始需要向前产生4m/s2的加速度，若此时想要在200ms以内关节电机能够控制下方底盘姿态达到目标姿态：此时考虑车体默认高度为0.1569m可得车体相对轮毂需要水平移动的距离为0.0801m，此时可以计算出两侧关节电机分别需要的角度为247.352°和151.882°，此时需要响应的平均角速度为ω=200msmax{∣247.15∘−200∘∣,∣151.882∘−200∘∣}=240.59∘/s=4.1991rad/s=40.09RPM

​ 在此基础上若考虑为控制器控制电机留出1倍的响应余量，此时需要电机实际至少达到80rpm的额定转速。

3.关节电机转速需求小结

​ 综合以上两种需求情况下的结论可以得出关节电机的额定转速大约在82rpm左右。

2.轮毂电机选型分析

​ 由于轮毂电机的选型相对比较简单，所以这里将受力计算与转速计算放在一起。

1.一般应用场景分析

​ 在轮腿步兵的需求下，轮毂电机的主要作用在于给车体产生水平方向上的加速度，目前的需求是机器人尽量能够在水平地面上产生水平方向4m/s2的加速度，所以总计需要两个轮毂电机输出总计f=ma=25.2kg×4m/s2=100.8N的水平摩擦力，此时换算成摩擦扭矩的过程种还需要考虑轮子的半径，如果能够保证轮子在路面不打滑的话需要的轮子半径其实是越大越好，但是考虑到轮子的实际重量，可以将轮子半径计算为10cm，那么此时需要轮毂电机输出的扭矩大致为M=2fr=5.04Nm。同时，如前所述，平衡步兵需要能够在平地上稳定保持6m/s的平移速度，在上述轮毂半径10cm的假设下我们可以计算得出此时的轮子转速大约为ω=rv=8cm5m/s=62.5rad/s=3582.8∘/s=597.1RPM，上述的计算过程中为轮子半径留出了大约20%的余量。

2.小陀螺情况分析

​ 由于轮腿步兵没有采用麦轮的结构，所以在理论上小陀螺转速可以达到一个比较快的程度且保持陀螺状态不太费电，假定想要实现轮腿步兵实现每秒2.5圈的小陀螺目标，由于轮腿步兵非麦轮传动的限制，此时轮腿步兵不能在小陀螺时进行移动，所以此时只需要考虑在水平地面上平衡步兵可以在1.5s内由静止达到2.5圈每秒的小陀螺状态。先从目标转速入手，此时需要电机输出端速度为ω=rv=r2πn2L=8cm2π×2.5r/s×20.6m=58.875rad/s=3375∘/s=562.5RPM。

​ 在此情况下，我们需要机器人在默认情况下能够在1.5s内达到目标转速，电机实际输出的总能量应该就是最终状态下步兵小陀螺具有的动能，所以这里首先考虑计算默认状态下的转动惯量，在如下图所示的平衡步兵简易模型中，可以将整个平衡步兵分为三个部分进行计算，即上层机构所在的板、两种不同的连杆，相关计算过程如下：

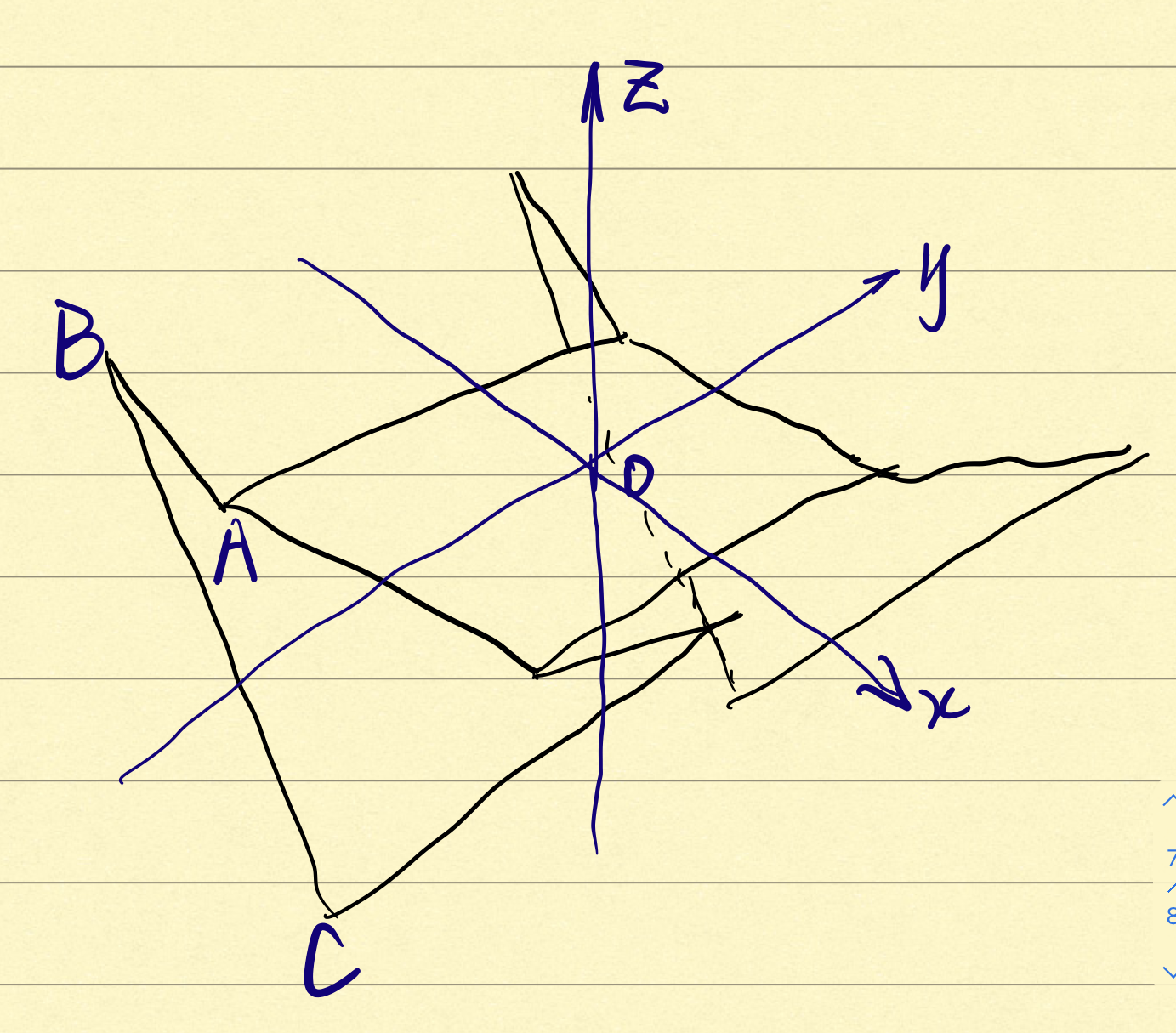
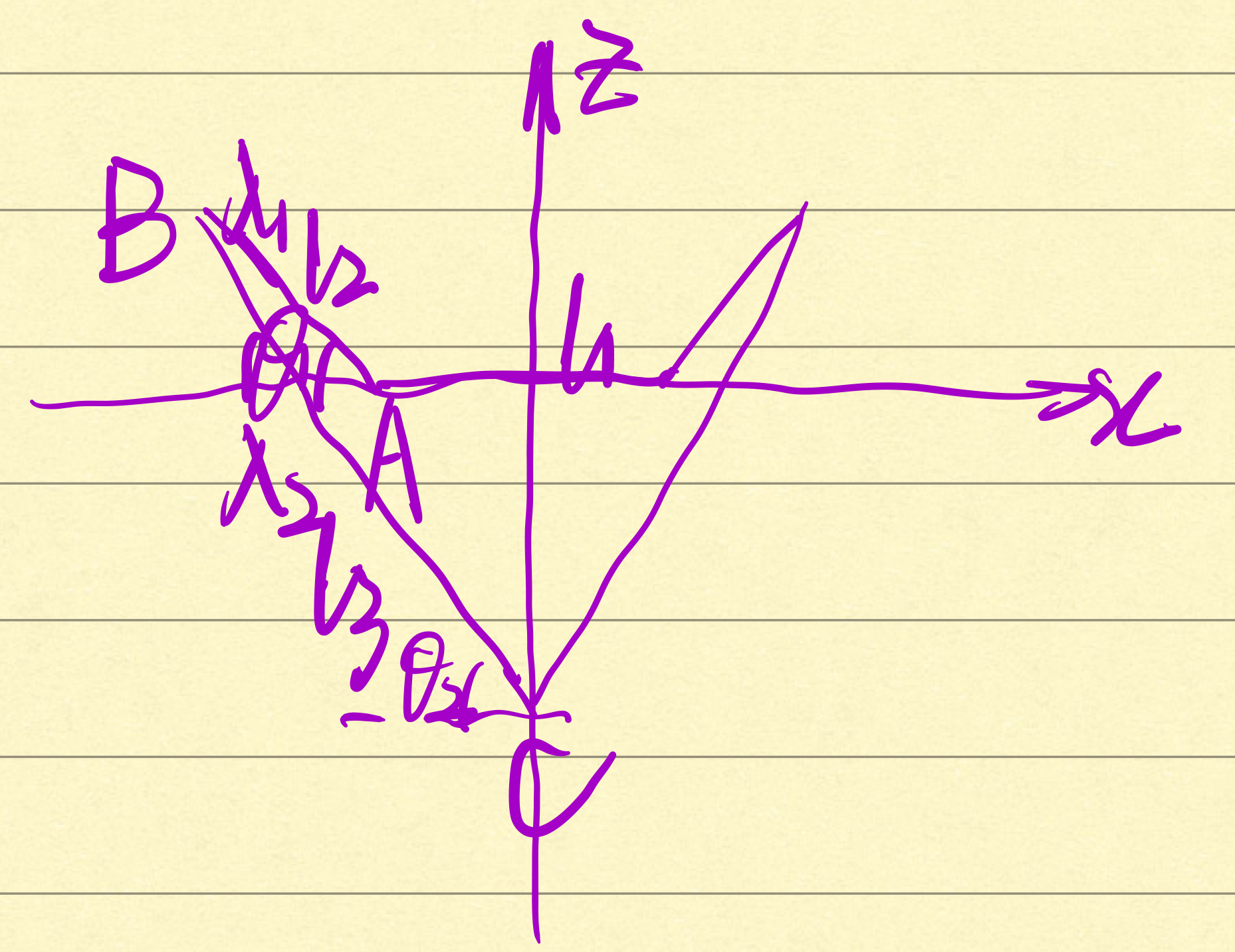
其中涉及的相关数据为：

​ 中间上层机构等效出来的四边形长和宽分别为L和l1/2；正常默认状态下θ1=20°，而θ2满足表达式

​ 腿部分在计算时考虑为质量分布均匀的线，其质量线密度为

.

​ 最终可以计算出该状态下沿z轴旋转的转动惯量：

​ 在此情况下若是想要达到每秒2.5圈的小陀螺转速，只需要计算出其总角动量和总动能：

​ 所以最终能够计算出，如果想要在1.5s内达成加速需求，此过程中的单电机的平均功率和平均输出扭矩分别为·：

3.飞坡/上坡情况分析

​ 实际比赛场地中存在非常多的坡道，所以在进行平衡步兵相关计算的时候不得不考虑针对坡道元素的相关计算。

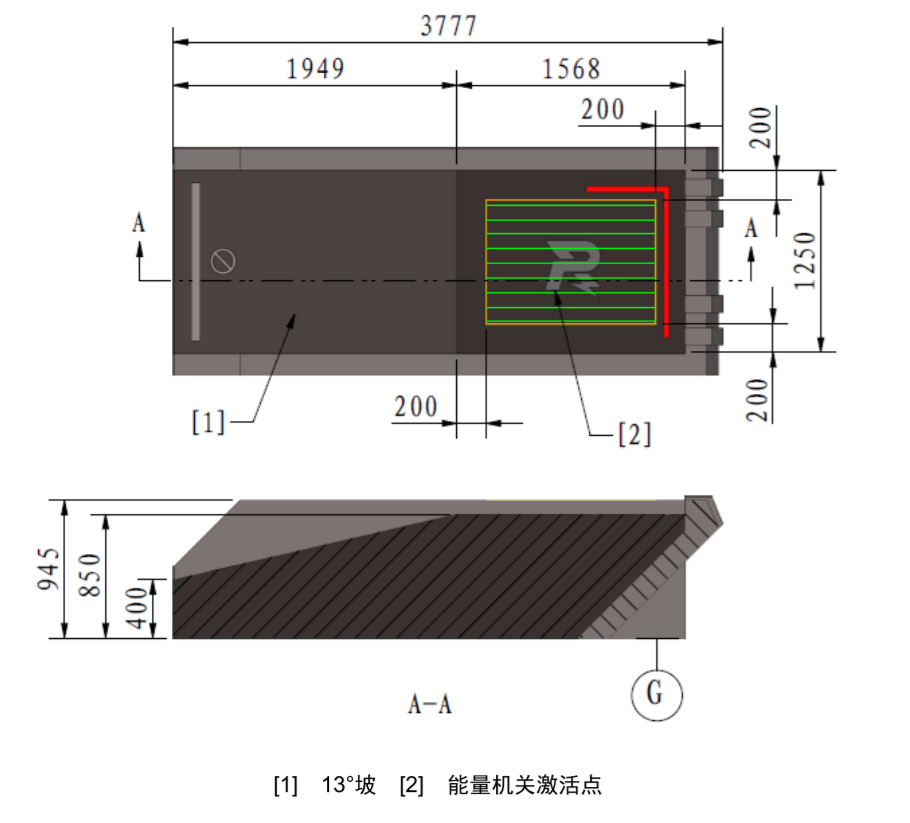
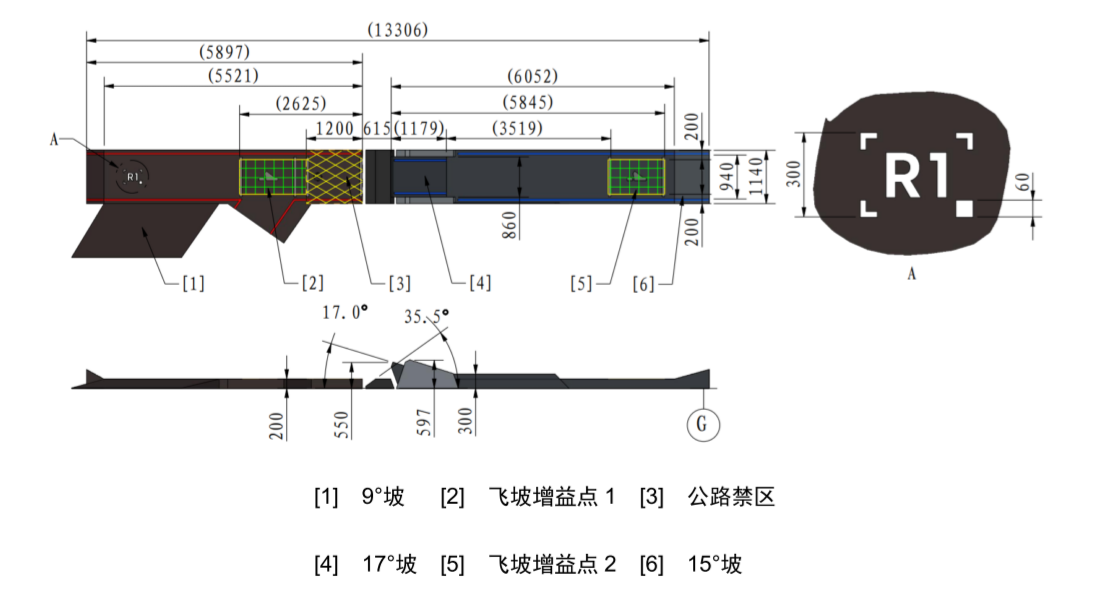
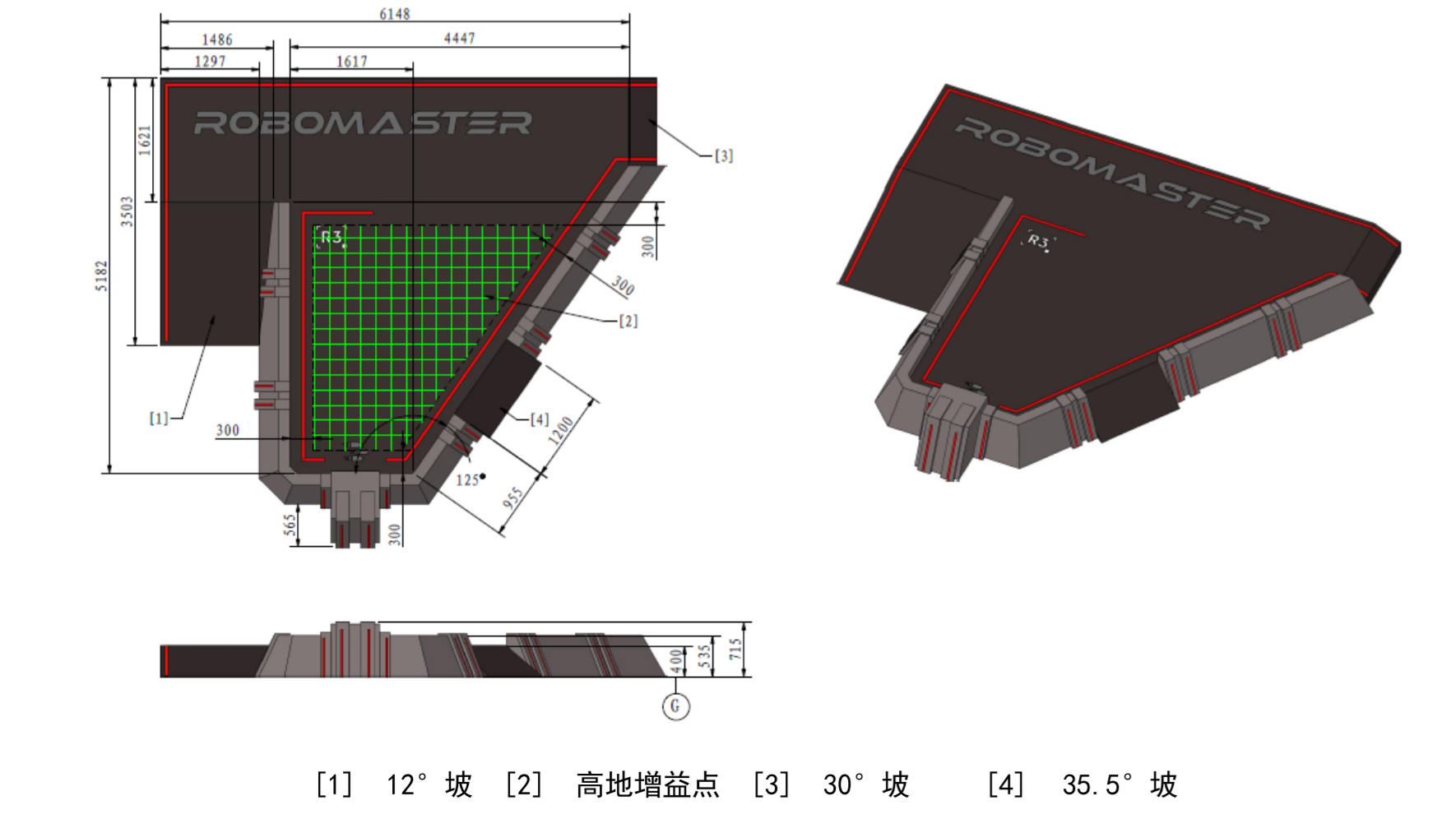
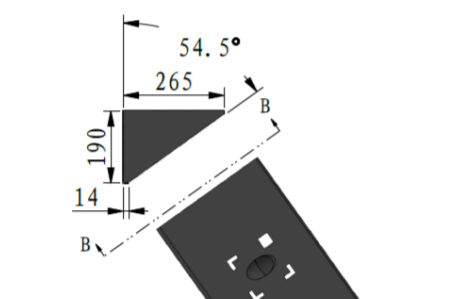
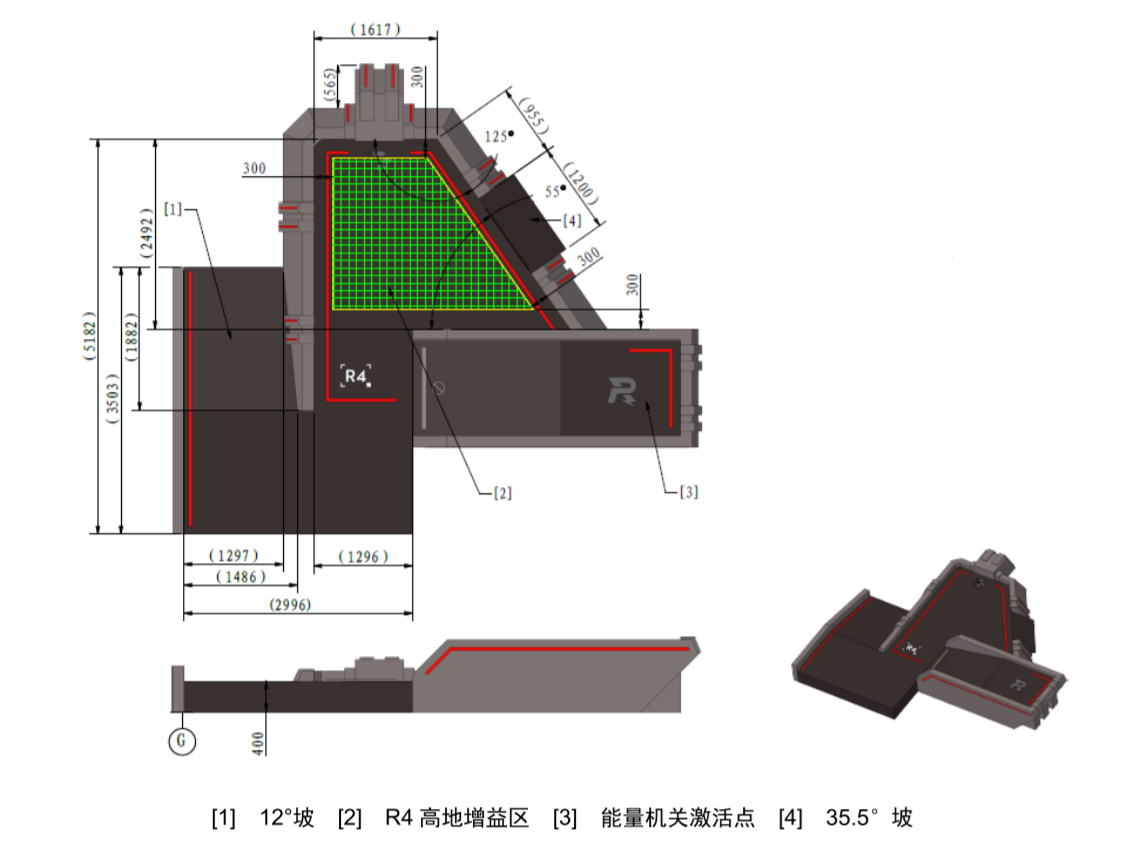
​ 翻看规则手册不难发现，场地中存在的坡度最大的坡道的坡度为35.5度。考虑到正压力减小造成的抓地力减小，实际上不需要在上坡的过程中保持比较大的水平加速度，只需要保证在坡上能够保证小加速度加速甚至只需要能够保证在坡上不减速即可。

​ 在35.5°的坡上，轮毂电机需要静态输出扭矩以抵消重力在坡上的分力以防止下滑，在我们讨论的情况下，该分力的大小为，此时每个轮毂电机都需要输出。

​ 考虑到这两个坡度都比较大，所以如果除开30°以及上的坡，在最大需求坡度为19°的情况下，每个轮毂电机都需要输出.

4.轮毂电机需求小结

​ 总的来说，轮毂电机的参数需求主要取决于驱动轮的半径，在驱动轮半径不大于10cm的情况下，轮毂电机的额定转速需求大约在600RPM，而轮毂电机的输出扭矩需求主要集中在是不是需要上35.5度的坡，在需要上35.5°的坡的情况下需要输出的扭矩大约是5Nm，如果需要上35.5°的坡，需要输出的扭矩就得达到7Nm。同时，考虑到轮毂电机的实际工作状态，该电机的输出端不能有虚位，以避免出现电机烧毁的情况。

3.轮腿步兵电机选型需求总结

关节电机选型过程中需要注意的点在于：

1. 输出扭矩不能小于15Nm，如果想要实现跳跃功能则不能小于22Nm；
2. 关节电机的转速需求大约82RPM；
3. 为了能够实现更加稳定的度过起伏路段，最好能够保证电机在减速后输出轴阻力比较小。

轮毂电机选型中需要注意的点在于：

1. 如果想要适应场地中的所有地形，轮毂电机的输出扭矩需要7Nm，如果放弃35.5°的坡大约只需要5Nm；
2. 轮毂电机输出额定转速大约为600RPM；
3. 为了保证轮毂电机能有比较好的控制效果，实际输出轴最好能是直驱或者配低背隙与阻力的减速箱。