四足机器人控制仿真（v-rep)

​ 以下基于v-rep学习，通过网上相关资料进行学习，进行总结输出。

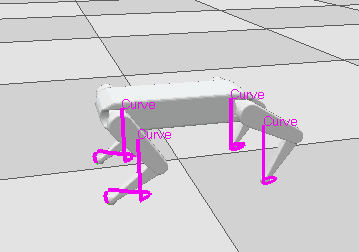
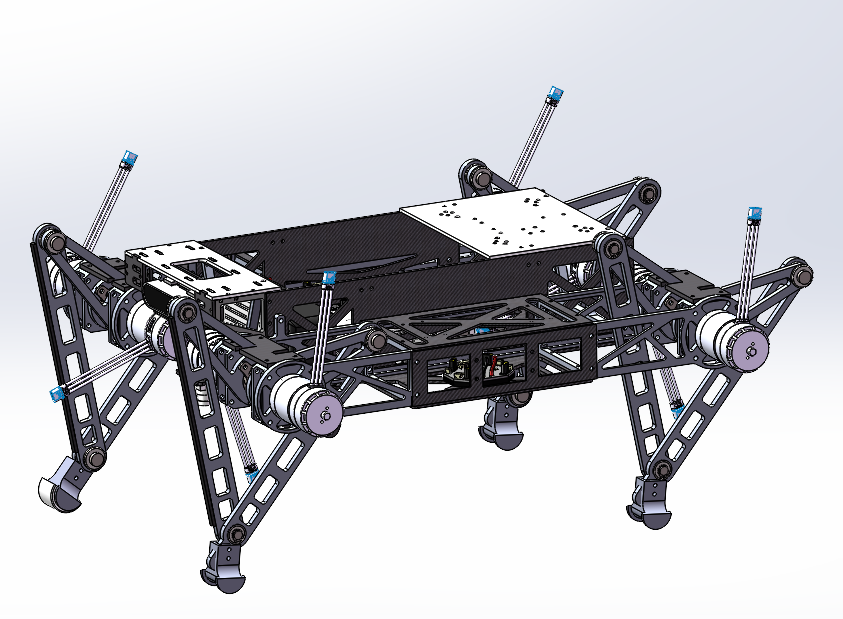
​ 先来一张之前画的并联腿的四足。这次仿真是串联腿的。

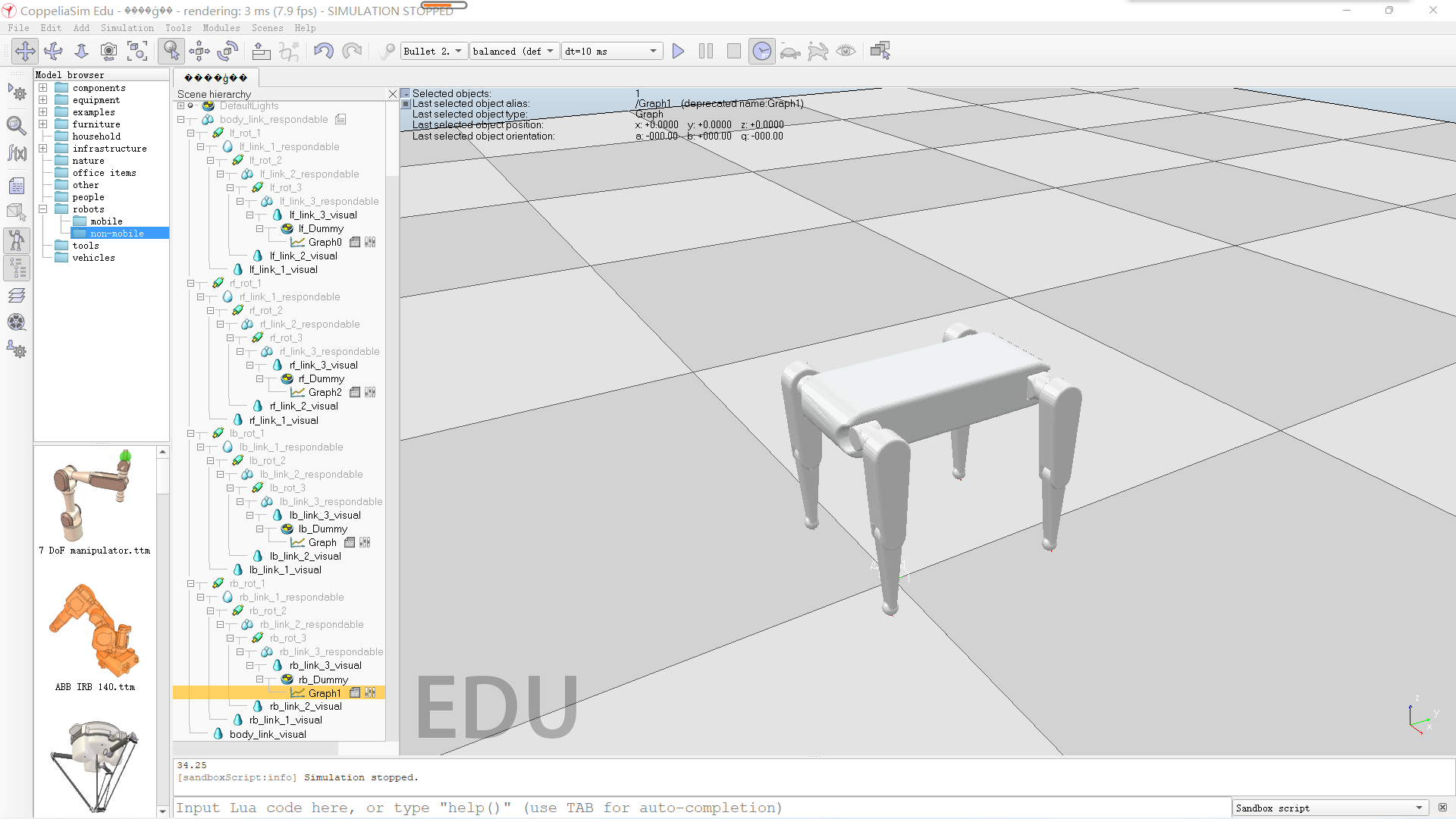
1.模型导入＋参数设置

在建立matlab和v-rep通信的时候，我遇到了一个报错，如下：

​ 配置C:\Program Files\CoppeliaRobotics\CoppeliaSimEdu\programming\remoteApiBindings\matlab\matlab中的文件后，运行CoppeliaSim，再运行MATLAB报错：

解决方案：

需要配置C:\Program Files\CoppeliaRobotics\CoppeliaSimEdu\programming\remoteApiBindings\lib\lib\Windows中的remoteApi.dll 一起复制到编译文件即可。

建立通讯代码

%通讯初始化
clear
clc
disp('Program started');
vrep=remApi('remoteApi'); 
vrep.simxFinish(-1); 
clientID=vrep.simxStart('127.0.0.1',19999,true,true,5000,5);  %如果返回值为-1 则代表通讯不成功,返回值为0代表通讯成功
disp(clientID);

2.单腿逆运动学求解

​ 通过几何关系求得，未用机器人工具箱函数，以往一直使用工具箱，导致自己求逆解过程都不熟悉了，以下为逆解matlab代码。

function [gamma,alfa,beta] = xyz(x,y,z)
h=0.15;
hu=0.35;
hl=0.382;
dyz=sqrt(y.^2+z.^2);
lyz=sqrt(dyz.^2-h.^2);
gamma_yz=-atan(y/z);
gamma_h_offset=-atan(h./lyz);
gamma=gamma_yz-gamma_h_offset;
%
lxzp=sqrt(lyz.^2+x.^2);
n=(lxzp.^2-hl.^2-hu.^2)/(2*hu);
beta=-acos(n/hl);

%
alfa_xzp=-atan(x/lyz);
alfa_off=acos((hu+n)/lxzp);
alfa=alfa_xzp+alfa_off;

%输出角度为弧度
end

3.站立姿态解算

function [rb_x,rb_y,rb_z,rf_x,rf_y,rf_z,lb_x,lb_y,lb_z,lf_x,lf_y,lf_z] = pose_control(row,pitch,yaw,pos_x,pos_y,pos_z)
b=0.4;
l=0.8;
w=0.7;
h=0.732;
R=row*pi/180   ;
P=pitch*pi/180 ;
Y=yaw*pi/180   ;
pos=[pos_x,pos_y,pos_z]';
rotx=([[ 1,        0,         0      ]
       [ 0,        cos(R),   -sin(R) ]
       [ 0,        sin(R),    cos(R) ]]);
roty=([[ cos(P),   0,        -sin(P) ]
       [ 0,        1,         0      ]
       [ sin(P),   0,         cos(P) ]]);
rotz=([[ cos(Y),  -sin(Y),    0      ]
       [ sin(Y),   cos(Y),    0      ]
       [ 0,        0,         1      ]]);
rot_mat = rotx * roty * rotz;
%结构参数
  body_struct = ([[ l / 2,  -b / 2,  h]     
                 [  l / 2, b / 2,   h]     
                 [ -l / 2,  b / 2,    h]     
                 [ -l / 2, -b / 2,   h]])'; 
             
 footpoint_struct = ([[ l/2,   -w/2,  0]
                     [  l/2,   w/2,  0]
                     [  -l/2,    w/2,  0]
                     [  -l/2,    -w/2,  0]])';
leg_pose = zeros(3, 4);
for i= 1:4
    leg_pose(:,i) =  pos + rot_mat * body_struct(:, i) - footpoint_struct(:, i);
end

 rb_x = (leg_pose(1, 1));
 rb_y = -(leg_pose(2, 1));
 rb_z = -(leg_pose(3, 1));
 rf_x = (leg_pose(1, 2));
 rf_y = (leg_pose(2, 2));
 rf_z = -(leg_pose(3, 2));
 lb_x = (leg_pose(1, 3));
 lb_y = (leg_pose(2, 3));
 lb_z = -(leg_pose(3, 3));
 lf_x = (leg_pose(1, 4));
 lf_y = -(leg_pose(2, 4));
 lf_z = -(leg_pose(3, 4));
end

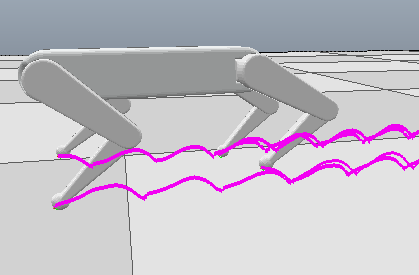
4.足端轨迹规划

初步学习用了最简单的摆线。

clc;
clear;
Ts=1;    %周期
xs=-0.1;    %起点x位置
xf=0.1;     %终点x位置
zs=-0.582;   %z起点位置
h=0.1;      %抬腿高度
x=[];
z=[];
for t=0:0.01:Ts
    sigma=2*pi*t/(Ts);
    xep=(xf-xs)*((sigma-sin(sigma))/(2*pi))+xs;
    zep=h*(1-cos(sigma))/2+zs;
    x=[x,xep];
    z=[z,zep];
end
plot(x,z,'r','LineWidth',3)

5.步态规划与仿真

​ 足式运动的步态是指腿的摆动和支撑运动以及这些运动之间的相对时间关系。不同的步态规则决定了不同的足式运动方式，从而形成了不同的步态形式。目前对步态的研究主要是为了实现机器人的稳定周期运动研究的重点是具体的步态规划方法。

​ 传统的步态规划内容包括了足端运动轨迹规划，以及协调腿和腿之间运动的相对时间关系，也就是步态时序。其中，足端运动轨迹还包含了摆动相轨迹和支撑相轨迹，两者决定了单个腿的运动特征;而规划不同的步态时序就对应了机器人整体的不同步态形式。
​ 按照平衡方式来分，四足机器人的步态可以分为静态步态(Static Gaits)、动态步态(Dynamic Gaits)和准静态步态(Quasi-static Gaits)三种。

walk步态

​ walk步态是静态步态，它的步态特征是任意时刻至多只有一条腿处于摆动相，四条腿按照一定的次序轮换向前摆动。四足动物在walk步态中最常用的轮换次序是1→3→4→2→1的倒“8”字型。

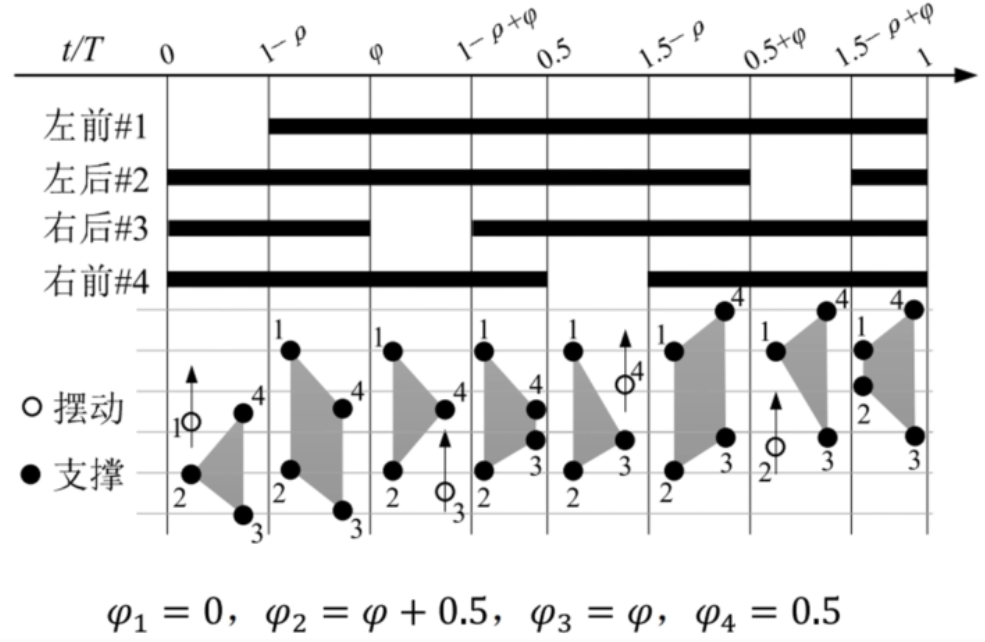
function [x,z] = gait_plan2(t,T)
Ts=T/4;  %周期为0.25s
xs=-0.1; %起点x位置
xf=0.1;  %终点x位置
zs=-0.482; %z起点位置
h=0.15;   %抬腿高度
if(t<=Ts)  
sigma=2*pi*t/Ts;  
x=(xf-xs)*((sigma-sin(sigma))/(2*pi))+xs;
z=h*(1-cos(sigma))/2+zs;
else
x=(-(xf-xs)/(T-Ts))*(t-Ts)+xf;
z=-0.482;
end
end

Trot步态

​ Trot步态适用于中低速跑动，并具有比较大的运动速度范围。另一个重要特点是,在中等速度下的Trot步态具有最高的能量效率。这些优点使得Trot步态成为最常用的四足步态Trot步态的特征是对角的两条腿成对运动，即腿1和腿3运动一致，腿2和腿4运动一致，理想情况下对角腿同时抬起并同时着地。Trot步态同样具有左右对称性，各腿的相位差为: φ1= 0，φ2= 0.5，φ3 = 0, φ4= 0.5

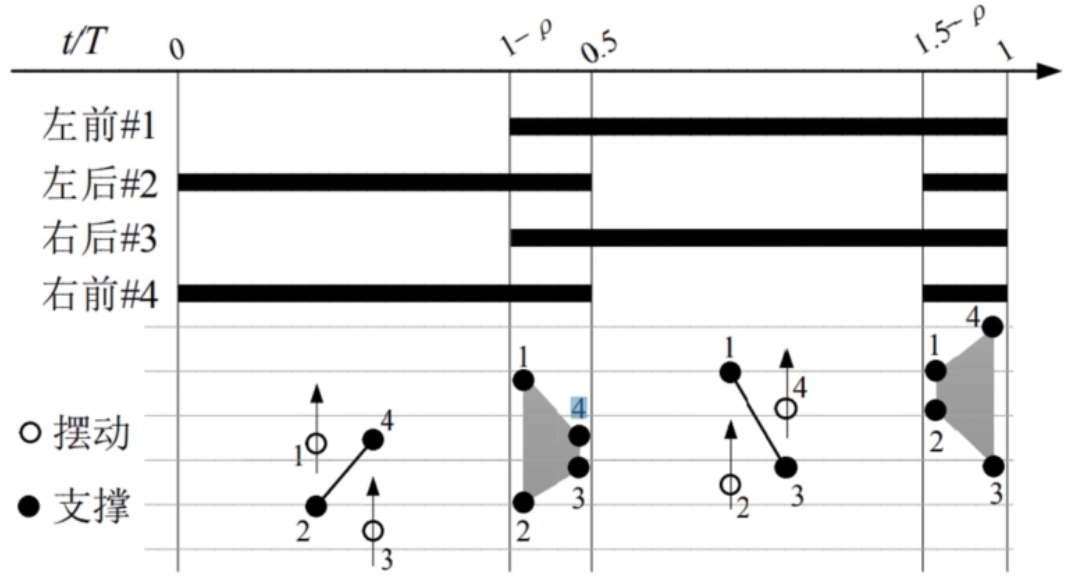
function [x,z] = gait_plan1(t,T)
Ts=T/2;  %周期为0.2s
xs=-0.1; %起点x位置
xf=0.1;  %终点x位置
zs=-0.482; %z起点位置
h=0.1;   %抬腿高度
if(t<=Ts)  
sigma=2*pi*t/Ts;  
x=(xf-xs)*((sigma-sin(sigma))/(2*pi))+xs;
z=h*(1-cos(sigma))/2+zs;
else
x=(-(xf-xs)/(T-Ts))*(t-Ts)+xf;
z=-0.482;
end
end