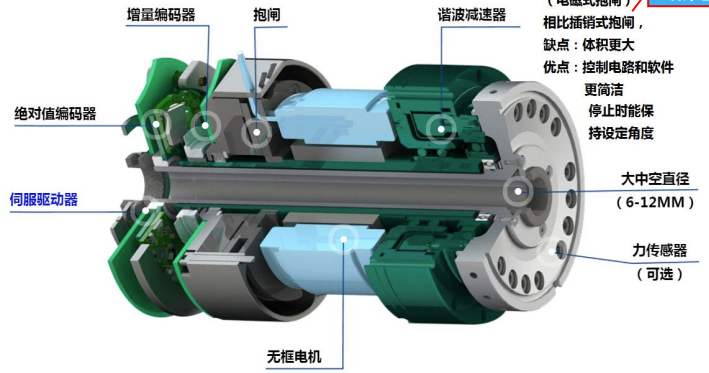
1.机械臂关节模组
1.1结构组成
| 机械臂关节模组 | 部件供应商 |
|---|---|
| 机械抱闸 | 德国TQ |
| 无框力矩电机 | 科尔摩根、德国TQ、泰科伺服、杭州精导 |
| 谐波减速器 | 绿的、来福、山卓等、日本Harmonic Drive 哈默纳科 |
| 光电编码器(减速器前,与电机构成伺服电机) | US digital、泰科伺服 |
| 绝对值编码器(减速器后,测量机械臂的输出轴绝对角度) | 尼康、多摩川、零差云控、英国尼绍、AMS |
| 伺服驱动器 | 德国赛普思、武汉迈信、中科深谷 |
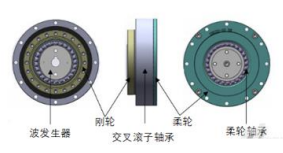
1.2谐波减速器
1.2.1原理
谐波减速器主要由波发生器、柔性齿轮、刚 性齿轮、柔性轴承、交叉滚子轴承等五个基本构件组成,是一种靠波发生器装配上柔性轴承 使柔性齿轮产生可控弹性变形,并与刚性齿轮相啮合来传递运动和动力的齿轮传动。谐波齿轮传动减速器是利用行星齿轮传动原理发展起来的一种新型减速器。
谐波减速器主要有以下三个基本构件:
➢ 带有内齿圈的刚性齿轮(刚轮),它相当于 行星系中的中心轮;
➢ 带有外齿圈的柔性齿轮(柔轮),它相当于 行星齿轮;
➢ 波发生器,它相当于行星架。
1.2.2主要特点
- 承载能力高,谐波传动中,齿与齿的啮合是面接触,加上同时啮合齿数(重叠系数)比较多(同时啮合的齿数占总齿数的约30%),因而单位面积载荷小,承载能力较其它传动形式高。
- 传动比大,双级谐波齿轮传动的传动比,可达i=30~320。
- 体积小、重量轻,与以往的齿轮装置相比,体积为1/3,重量为1/2,却能获得相同的转矩容量和减速比,实现小型轻量化,尤其适合机器人使用。
- 传动效率高、寿命长。
- 传动平稳、无冲击,噪音低,齿隙小,运动精度高。
- 零部件少、安装简便 。
- 缺点:由于柔轮承受较大的交变载荷,因而对柔轮材料的抗疲劳强度、加工和热处理要求较高,柔轮材料使用疲劳强度大的特殊钢,工艺复杂,造价昂贵。
1.3无框力矩电机
1.3.1主要特点
➢ 控制精准:转矩脉动极低,扭矩和电流线性度好,易于速度控制和精确位置定位控制
➢ 响应快速:转动惯量小、动态响应快、具有优异的动态性能
➢ 结构紧凑、功率密度高:定转子结构紧凑,转子采用高性能稀土永磁材料
➢ 散热性能好:散热好、绝缘佳
➢ 大中空孔径:中空大孔径,可以进行中间走线
1.4绝对值编码器
➢ 测量机械臂关节末端的绝对值角度
➢ 标定绝对零点
➢ 采用BISS协议与驱动器进行通讯
➢ 上电驱动器和控制器就能获得机械臂关节的角度。
➢ 该编码器不能进行多圈测量,可选用尼康、 多摩川等编码器实现多圈的角度的测量,不过通常需要额外增加电池供电,断电才不会丢失圈数信息
2.机械臂分析
2.1引言
机械臂的运动学分析在整个仿真过程中是十分重要的,机械臂的运动学建模及轨迹跟踪是机械臂控制的基础,在此之上才能使用机械臂完成高精度的力/位置控制。机械臂运动学可以分为两个方面,正运动学和逆运动学,正运动学研究的是在已知关节角度和连杆参数的情况下求取末端在空间中的位姿﹐机械臂逆运动学求解与正运动学求解相反,它是在已知机械臂末端空间位姿和连杆参数的情况下求取各个关节角度[12]。本文将以UR5机械臂(如图2-1所示〉作为研究对象,建立机械臂运动学模型。

图2-1 UR5机械臂
2.2机械臂运动学建模
2.2.1 D-H法
六自由度UR5机械臂由六个转动关节和连杆组成,关节之间使用刚性连杆连接。Denavit和Hartenberg 于1955年提出可以使用D-H方法建立机器人运动学模型[13],D-H方法的具体思路是先分别在各关节建立关节坐标系,确定关节间刚性连杆参数,再依次将关节变化联系起来,计算出机械臂末端相对于基坐标系的变化关系,进而建立机械臂运动学方程。
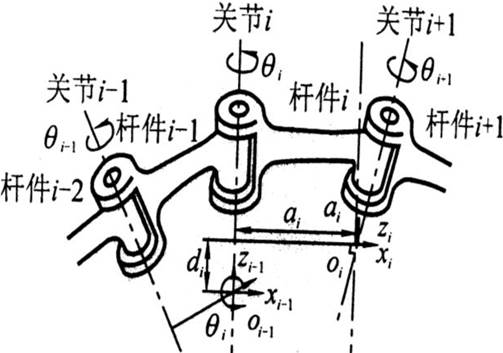
图2-2机械臂连杆参数
如图2-2所示,D-H法步骤如下:
(1)建立连杆坐标系,机械臂连杆指的是连接两关节之间刚性杆件,在建立机械臂连杆坐标系时,关节i的前一个连杆命名为连杆i-1,关节i的后一个连杆命名为连杆i,关节i与关节i+1公垂线的交点定义为连杆i坐标系原点[14]。
(2)描述连杆参数,关节i的轴线与关节i+1的轴线公垂线的长度定义为连杆i的长度;相邻两连杆延长线的交点与关节的轴线平行,关节轴线与连杆延长线垂直,关节角度指的是关节两侧轴线形成的夹角;关节偏置指的是连杆两侧关节的公垂线与在连杆轴线方向上的长度[15]。
(3)坐标系变换,根据连杆坐标系和关节角度,分别求出平移变换矩阵和旋转变换矩阵[16]。
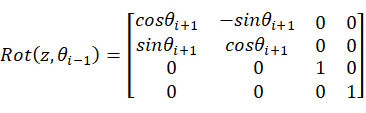
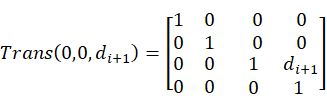
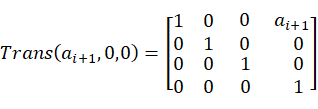
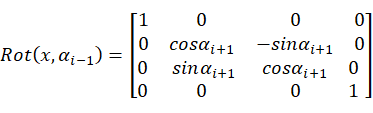
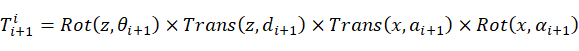
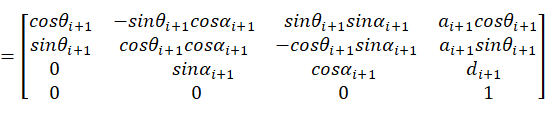
2.2机械臂运动学分析
2.2.1 UR5机器人坐标系建立
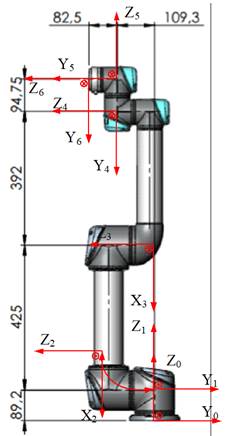
图2.2.1 UR5机器人坐标系
根据建立的UR5机器人坐标系,确定UR5机器人的D-H参数如表1所示。
表1 UR5机器人的D-H参数
Tab.1 D-H Parameters of the UR5 Robot
| i | 扭转角(αi-1) | 杆长(ai-1) | 关节偏距(di) | 关节转角(θi) |
|---|---|---|---|---|
| 1 | 0 | 0 | 89.2 | θ1 |
| 2 | 90 | 0 | 0 | θ2 |
| 3 | 0 | -425 | 0 | θ3 |
| 4 | 0 | -392 | 109.3 | θ4 |
| 5 | 90 | 0 | 94.75 | θ5 |
| 6 | -90 | 0 | 82.5 | θ6 |
根据公式得:
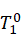 =
=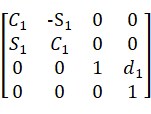
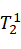 =
=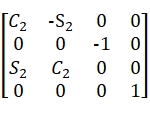
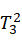 =
=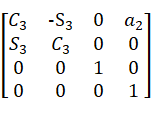
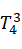 =
=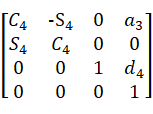
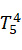 =
=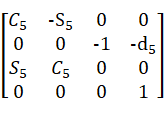
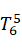 =
=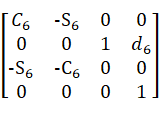
 ;
;
 =T_tool;
=T_tool;
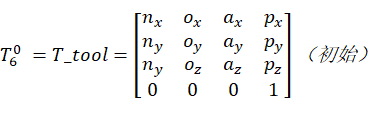 ,两边同时左乘以(
,两边同时左乘以(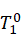 )-1,得
)-1,得
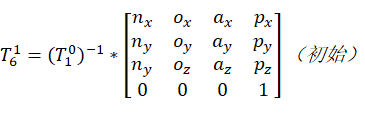 ,
,
其中,
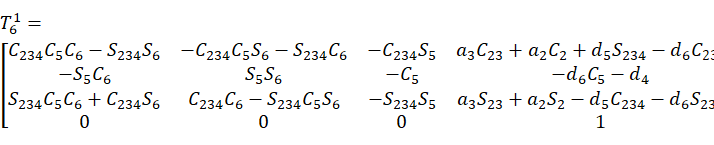 由于没有常数项,现将其DH参数做一下更改
由于没有常数项,现将其DH参数做一下更改
| i | 扭转角(αi-1) | 杆长(ai-1) | 关节偏距(di) | 关节转角(θi) |
|---|---|---|---|---|
| 1 | 0 | 0 | 89.2 | θ1 |
| 2 | 90 | 0 | 0 | θ2 |
| 3 | 0 | -425 | 0 | θ3 |
| 4 | 0 | -392 | 109.3 | θ4 |
| 5 | 90 | 0 | 94.75 | θ5 |
| 6 | -90 | 0 | 0 | θ6 |
| 7 | 0 | 0 | 82.5 | 0 |
即令d6 = 0;
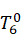 _new *
_new * 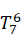 = T_tool;
= T_tool;
则
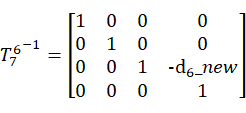
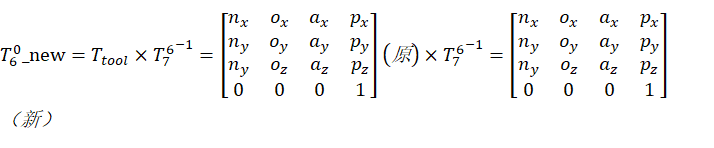 以下将最新去除默认为最新位姿矩阵。
以下将最新去除默认为最新位姿矩阵。
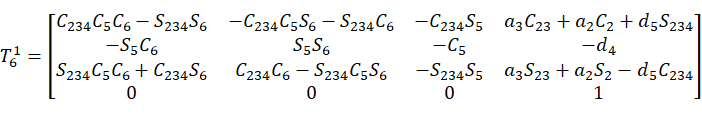
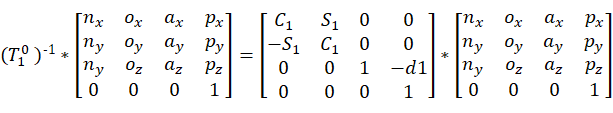
等式两边(2,4)相等得到:
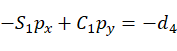 (1)
(1)
由万能公式得:
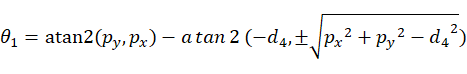
为求解结果,必须有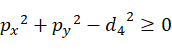 ,这样才能有解。
,这样才能有解。
等式两边(2,1),(2,2),(2,3)对应相等得到:
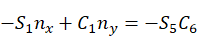 (2)
(2)
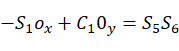 (3)
(3)
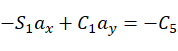 (4)
(4)
由等式(2),(3)得:
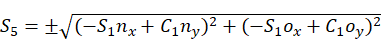 (5)
(5)
由等式(4),(5)得:
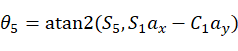
当S5=0时,即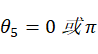 ,此时机构发生奇异,无法求出
,此时机构发生奇异,无法求出 。
。
由等式(2)(3)得:
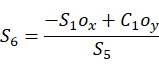
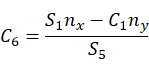
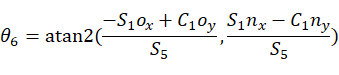
对比矩阵(1,3),(3,3)得:
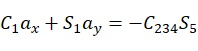 (6)
(6)
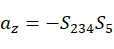 (7)
(7)
得到:
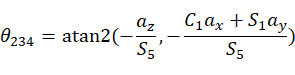
对比矩阵两边元素(1,4),(3,4)
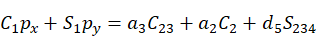 (8)
(8)
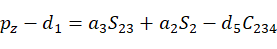 (9)
(9)
消去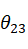 ,化简为:
,化简为:
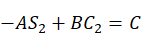 (10)
(10)
式中:
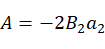
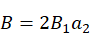
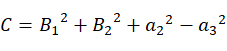
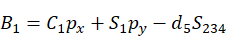
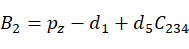
根据等式(10),依据万能公式:

为了求解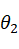 ,必须有
,必须有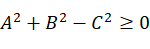 ,才有解。
,才有解。
求解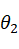 后,代入等式(8),(9)得:
后,代入等式(8),(9)得:
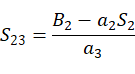
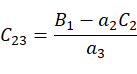
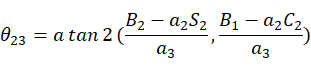
根据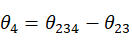 ,
,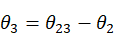 可得出其余两个关节角。
可得出其余两个关节角。
2.3 UR5机器人奇异性分析
奇异位形是机器人机构学中重要的运动学特性[17]。当机器人处于奇异位形时,末端执行器的位移或旋转运动受到限制。此时,机器人一般实际可操作自由度会减少,末端执行器不能实现某些方向的运动,也会出现某些关节角速度趋于无穷,导致机械手运动失控,机器人不能实现预定的动作[18]。严重影响机器人运动的稳定性,所以奇异位形分析对机器人平稳安全运动具有重要意义[19]。
对于UR构型的机械臂而言,它有三种奇异位型,通常是以奇异位型处的奇异点作为机械臂关节状态临界点,又可以将机械臂分为2种关节状态属性,这样三种奇异位型就可以产生出机械臂的8种关节状态属性,也就是8种运动学逆解。
UR构型机械臂的3种奇异位型按照奇异点的位置,可以将其分别表示为肩部奇异、肘部奇异以及腕部奇异,以下是对各奇异位型的描述:
当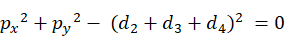 时,会导致肩部奇异,此时机械臂末端连杆坐标系的原点O6位于关节1轴线Z1和关节2轴线Z2所构成的平面内,
时,会导致肩部奇异,此时机械臂末端连杆坐标系的原点O6位于关节1轴线Z1和关节2轴线Z2所构成的平面内,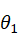 无法求解,当机器人运动到此处时,可导致控制过程中机械臂关节1的角度突变。
无法求解,当机器人运动到此处时,可导致控制过程中机械臂关节1的角度突变。
当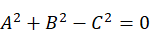 时,会导致肘部奇异,此时关节轴线Z2、Z3、Z4共面,
时,会导致肘部奇异,此时关节轴线Z2、Z3、Z4共面,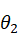 无法求解,当机器人运动到此处时,可导致控制过程中机械臂关节2的角度发生突变。
无法求解,当机器人运动到此处时,可导致控制过程中机械臂关节2的角度发生突变。
当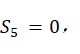 即
即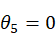 或者
或者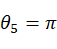 时,会导致机械臂的腕部奇异,此时轴线Z4和Z6平行,
时,会导致机械臂的腕部奇异,此时轴线Z4和Z6平行, 无法求解,当机器人运动到此处附件时,可导致控制过程中机械臂关节6的角度突变。
无法求解,当机器人运动到此处附件时,可导致控制过程中机械臂关节6的角度突变。
2.4机械臂运动学仿真验证
上一节对于UR5机器人的运动学进行了分析,但是还需要通过仿真来验证其正确性。本节通过MATLAB/SIMULINK仿真来对建立的运动学模型进行验证。MATLAB是由美国的MathWorks公司出品的商业数学软件,提供了数据可视化、算法开发、数据分析以及数值计算的高级计算语言和交互式环境。它将矩阵计算、数值分析、数据的科学可视化以及非线性动态系统的建模与仿真等很多非常强大的功能集成在一个视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案[20]。
2.4.1UR5机器人的正解验证
将建立的正解模型搭建在SIMULINK中,仿真模型如图2-2所示。
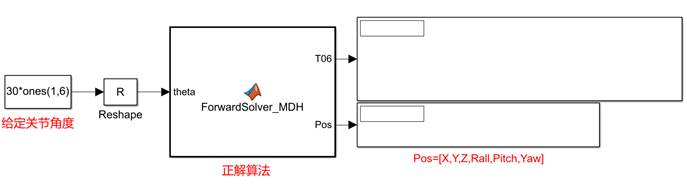
图2.2.1 UR5机器人正解模型
正解研究的是在已知关节角度和连杆参数的情况下求取末端在空间中的位姿。得到的结果如图2-3所示
得到的结果如图2-3所示
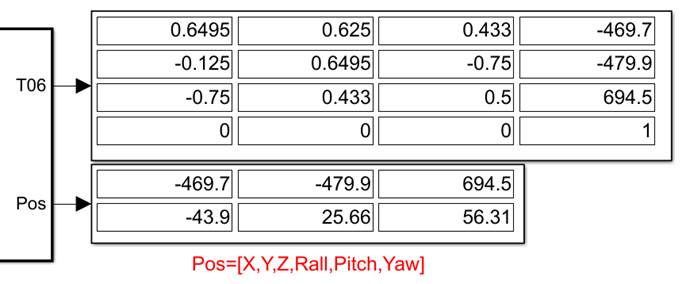
图2.2.1 UR5机器人正解模型结果
图2.2.1 UR5机器人工具箱正解结果
与机器人工具箱得到的正解结果进行比对,可知所建立的UR5运动学正解模型正确。
2.4.2UR5机器人的逆解验证
将建立的逆解模型搭建在SIMULINK中,仿真模型如图2-2所示。
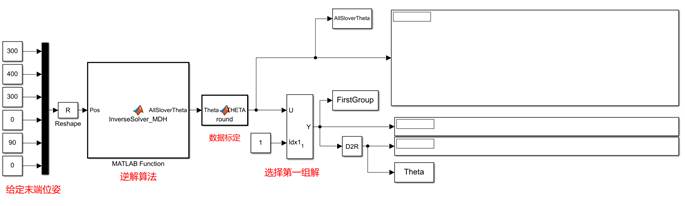
图2.2.1 UR5机器人逆解模型
与正解相反,逆解是在已知机械臂末端空间位姿和连杆参数的情况下求取各个关节角度,对于逆解的验证,可以指定机器人的末端按照规划的轨迹运动一段距离,这样就可以得到机器人每个电机转动的转角的信息。得到的结果如图2-3所示
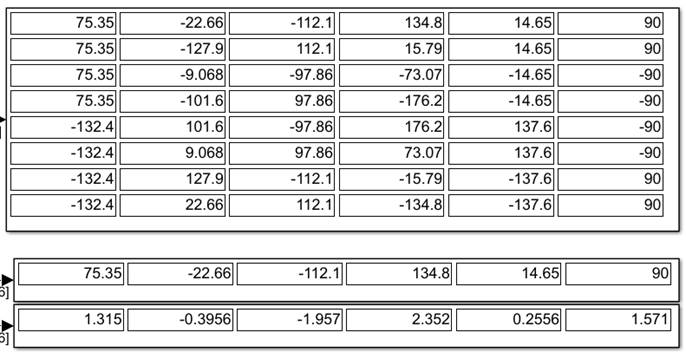
图2.2.1 UR5机器人逆解模型结果
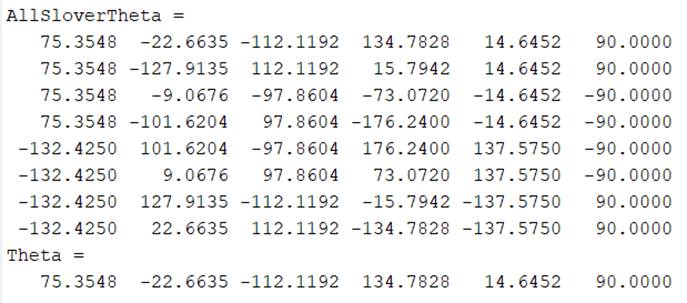
图2.2.1 UR5机器人工具箱逆解结果
与机器人工具箱得到的逆解结果进行比对,可知所建立的UR5运动学逆解模型正确。
2.5机械臂动力学建模
引言
机械臂动力学建模具有很大的意义,但目前国内很多机械臂的创业型公司,只实现了简单了轨迹控制,大部分都停留在通过示教器示教编程轨迹,然后再复现轨迹。这种传统的做法,的确是可以满足目前机械臂市场80%以上的应用场景,但对于复杂的场景,比如力控,牵引示教,高速高精度等场景,仅仅是基于运动学还是无法满足的,这便是机械臂动力学建模的意义之所在。
机械臂动力学建模主要是为了获取机械臂运动过程中的关节力矩,有四个目的,其一,将运动过程中的关节力矩通过前馈的方式补偿到驱动器三环控制中的最内环电流环,从而提高驱动器的响应速度进而提高机械臂的高速高精控制;第二,碰撞检测,机械臂在运动过程中,在没有外力时候的关节电流是可以通过实时计算关节力矩近似获得的,一旦驱动器电流环的电流瞬间变大,且远超出近似计算获得的电流值,此时可以判断机械臂发生了碰撞,控制器内部程序可以中断当前规划轨迹的运行。第三,机械臂力控制,通过设定机械臂的末端输出力矩,让机械臂以某一力矩作用在被作用对象上。第四,牵引示教,这是协作型机械臂的必备功能,通过给机械臂施加某一外力,让机械臂沿着外力方向运动。 机械臂的动力学建模目前比较普遍的方法有两种,一种是通过拉格朗日方程进行系统性建模,另一种是通过牛顿欧拉公式进行递推建模,两种方法最终的计算结果一致,但就计算的复杂度而言,关节越多牛顿欧拉方法越具有优势,同时牛顿欧拉递推法在编程实现上也比拉格朗日法更为简单。本文将通过牛顿欧拉递推法对UR5六轴机械臂进行动力学建模。
建模
在上一章中,介绍了UR5机械臂的运动学模型,假设采用前面的UR5机械臂模型参数,对UR5机械臂进行动力学建模。
则各连杆坐标系相对于前连杆坐标系的位姿矩阵如下所示:
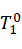 =
=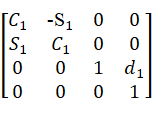
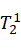 =
=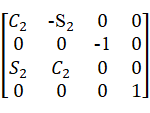
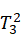 =
=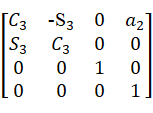
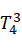 =
=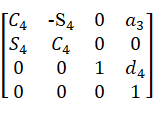
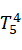 =
=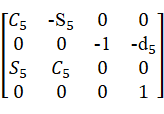
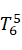 =
=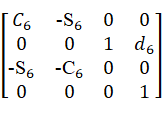
通过将上式中各连杆的位姿矩阵进行位置和姿态分离,可以得到六个连杆坐标系的旋转矩阵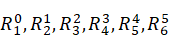 和位置坐标
和位置坐标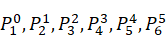 。
。
假设某一时刻连杆i坐标系和基坐标系固连,由基坐标系向连杆i坐标系递推连杆i在自身坐标系下的角速度,则有:
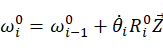 (1)
(1)
将连杆i在基坐标系下的角速度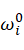 转换到连杆i自身动坐标系下的角速度:
转换到连杆i自身动坐标系下的角速度:
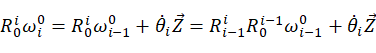 (2)
(2)
令 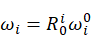 ,则有:
,则有:
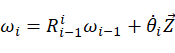 (3)
(3)
上式中,轴向量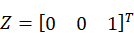 ,旋转矩阵
,旋转矩阵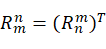 。
。
对公式(3)中的角速度进行求导可以得到各连杆的角加速度为:
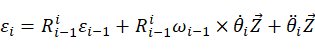 (4)
(4)
假设机械臂正装,也就是机械臂的基坐标系的Z轴方向和重力加速度的方向平行且反向,则基座的加速度为量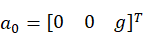 。由于某一时刻连杆i坐标系和基坐标系固连,由基坐标系向连杆i坐标系递推连杆i在自身坐标系下的角速度,则有:
。由于某一时刻连杆i坐标系和基坐标系固连,由基坐标系向连杆i坐标系递推连杆i在自身坐标系下的角速度,则有:
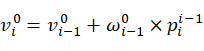 (5)
(5)
将连杆i在基坐标系下的线速度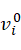 转换到连杆i自身动坐标系下的线速度:
转换到连杆i自身动坐标系下的线速度:
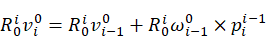 (6)
(6)
同样,令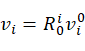 ,则有:
,则有:
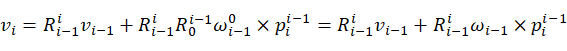 (7)
(7)
化简上式:
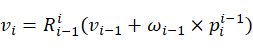 (8)
(8)
对上式进行求导可以得到:
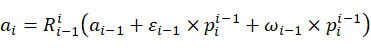
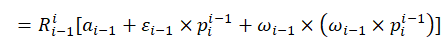 (9)
(9)
假设连杆i质心处的加速度为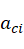 ,连杆i质心在连杆i坐标系下的位置为
,连杆i质心在连杆i坐标系下的位置为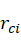 ,连杆i的质量为
,连杆i的质量为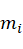 ,则有:
,则有:
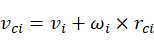 (10)
(10)
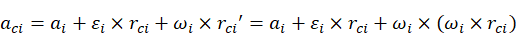 (11)
(11)
因此,可以得出连杆i的合力为:
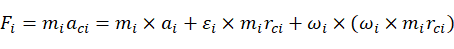 (12)
(12)
由叉乘公式可以得到:
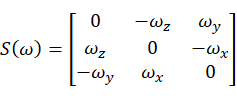 (13)
(13)
化简公式(12)可以得到连杆i的合力为:
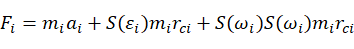 (14)
(14)
由欧拉方程可以得到连杆i的合力矩为:
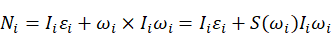 (15)
(15)
注意,上式中合力矩向量是连杆坐标系i下的力矩,连杆i惯性矩阵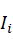 不是连杆质心上的惯性矩阵,而是连杆i坐标系下的惯性矩阵。
不是连杆质心上的惯性矩阵,而是连杆i坐标系下的惯性矩阵。
将连杆作为受力分析的研究对象,由机械臂末端连杆开始向机械臂基座连杆递推,分析机械臂的各关节受力。
对连杆i列力平衡方程,则其在基坐标下合力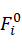 为:
为:
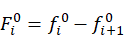 (16)
(16)
将其转换到自身的动坐标系下:
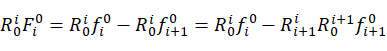 (17)
(17)
令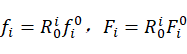 ,则有连杆i坐标系下的合力
,则有连杆i坐标系下的合力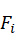 为:
为:
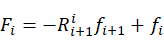 (18)
(18)
则连杆i所受外力为:
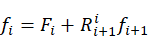 (19)
(19)
对连杆i列力矩平衡方程,基坐标系下的合力矩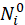 为:
为:
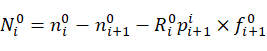 (20)
(20)
同样,将转矩从基坐标转换到连杆i自身的动坐标系下:
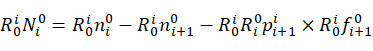 (21)
(21)
令,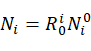 ,则有连杆i坐标系下的合力矩
,则有连杆i坐标系下的合力矩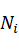 为:
为:
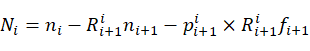 (22)
(22)
则关节i所受力矩为:
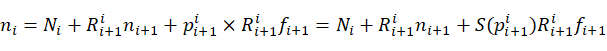 (23)
(23)
联立公式(14),(19),可以得到:
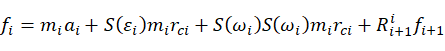 (24)
(24)
联立公式(15),(23),可以得到:
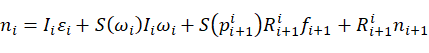 (25)
(25)
当机器人末端不受外力作用时,
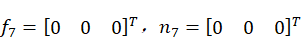 (26)
(26)
将式(26)代入到(24),(25),可以得到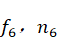 ,如此反复代入即可求得所有的关节所受到的力和力矩。
,如此反复代入即可求得所有的关节所受到的力和力矩。
动力学Simscape模型
2.5.1基于Simscape Multibody的仿真模型
机器人的动力学仿真常用的工具有Adams,V-REP,Gazebo等。本文采用Simscape Multibody 工具箱[21]来进行机械臂模型的快速搭建。通过Simscape Multibody Link插件[22]从SolidWorks 中直接获得实体模块,模型的导入过程十分方便,而且如果SolidWorks中的装配体中各个零件之间约束关系的定义是正确的,那么可以直接得到装配体中上述每一个分离的实体和关节模块。这样最后对生成的模块进行微调和自定义,就可以得到合适的仿真模型。

图2.2.1 Solidworks中绘制的模型
在SolidWorks中绘制好UR5的装配体,如图2-2,经过上述工具导入Simulink 后如图2-3所示。可以从图2-3中看出机器人的实体主要被分成了两种模块:实体(bodies)、关节(joints)。在生成模型的同时还生成了该模型的初始化的配置文件,该文件定义了模型中所有的坐标系之间的关系,所有零件的惯性矩阵、质心位置、关节的初始位置等,可以直接通过修改其中的文件参数并重新加载模型来满足自定义的需求,这对于通过已有三维模型的装配体而进行仿真是非常方便的。
,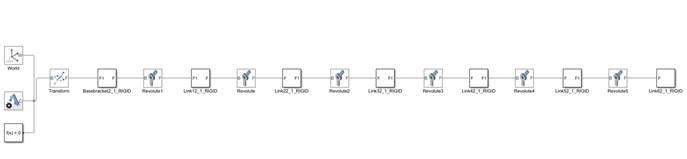
图2.2.1 导入后的Simscape模型
将修改初始化参数后的图2-3所述模型封装成子模块如图2-4(a)所示,从图中可以看出该模块有力矩输入、角度输出、角速度输出、检测力矩输出和机器人受到的接触力输出。运行之后的模型如图2-4(b)所示,图中对应着图2-3中的各个模块的可视化。
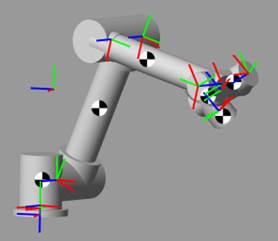
图2.2.1 Simscape模型运行可视化效果
2.6机械臂的位置轨迹规划
本文只研究笛卡尔空间的轨迹规划,在机械臂的笛卡尔空间轨迹规划中,中间点即插补点的坐标可以通过插补算法得到。得到中间点后,在把中间点的位姿转换成相应的关节角,再通过对关节角的控制,使得机械臂的末端能按照预先规划的路径运动。机械臂的笛卡尔空间轨迹规划位姿控制过程大致如图2.3所示。
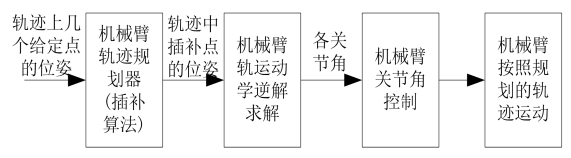
图2.2.1 笛卡尔空间轨迹规划位姿控制过程
空间直线和空间弧线的轨迹规划是笛卡尔空间中不可或缺的两部分,也是本文下文阻抗控制仿真中所规划的两种轨迹。因为空间的曲线可以分割为许多直线和弧线;但是也有会出现直线或弧线连接处尖角问题,为了使运动轨迹连续平滑,本文采用圆弧过度来平滑尖角。在笛卡尔空间中,空间直线和空间弧线的轨迹规划是最常见的两部分,其他空间曲线可以通过这两者来逼近。
2.6.1空间直线轨迹规划
空间直线插补就是在该直线起始点和终止点位姿已知的情况下,对轨迹中间点(插补点)的位姿坐标进行求解。
直线插补法(线性插补):
已知起始点位置坐标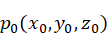 、终止点位置坐标
、终止点位置坐标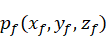 和插补次数N,则:
和插补次数N,则:
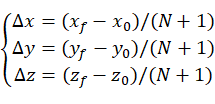
对于该直线上的任意一点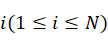 有:
有:
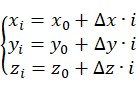
通过MATLAB搭建空间直线插值算法,得到结果如图2.4。
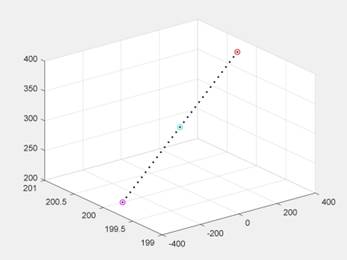
图2.2.1 直线插值算法结果
借助MATLAB机器人工具箱进行机械臂笛卡尔空间直线轨迹动态仿真,结果如图2.5。
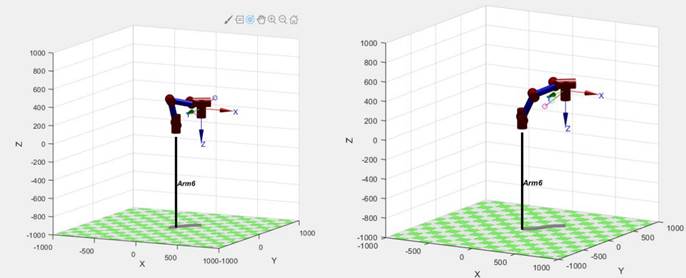
图2.2.1 笛卡尔空间直线轨迹规划仿真
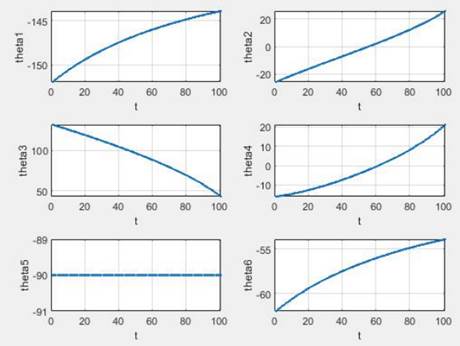
图2.2.1 笛卡尔空间直线轨迹规划关节角度变化曲线
2.6.1空间圆弧轨迹规划
在笛卡尔空间圆弧轨迹规划中,为了计算方便,运用坐标变换,即先在圆弧所在平面建立一个新的直角坐标系,在这个直角坐标系中计算圆弧的各插补点在新坐标系中的值。然后再将这些值返回到原来的坐标系中,算出各插补点在原来坐标系中的值。圆弧插补的位移曲线也是采用抛物线过度的线性函数,归一化因子的求解与上述一样。
三点确定一段弧。设机械臂末端执行器从起始位置P1经过中间点P2到达终点P3,如果这三点不共线,就一定存在从起始点P1经过中间点P2到达终点P3的圆弧轨迹规划算法。通过将空间点转换到二维平面,可将三维空间问题变为二维平面问题。具体算法如下:
构造新坐标系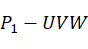 ,以
,以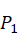 为坐标原点,以
为坐标原点,以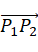 为U轴,以空间三点平面法向量为W轴,再通过U和W轴叉积得V轴。
为U轴,以空间三点平面法向量为W轴,再通过U和W轴叉积得V轴。
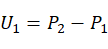
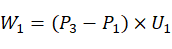
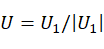
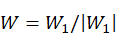
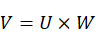
再将空间三点转换到新坐标系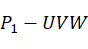 (
(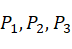 在新坐标系上表示为A,B,C),并计算圆心。
在新坐标系上表示为A,B,C),并计算圆心。
在坐标系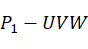 中,点A为圆心,坐标为(0,0),点B在U轴上,坐标为(bx,0),点C坐标为(cx,cy)。通过向量点积可以求得点
中,点A为圆心,坐标为(0,0),点B在U轴上,坐标为(bx,0),点C坐标为(cx,cy)。通过向量点积可以求得点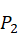 和
和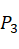 在U,V轴上投影。
在U,V轴上投影。
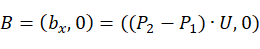
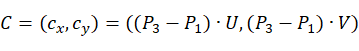
根据A,B,C三点位置可知,圆心必定落在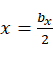 的直线上,因此设圆心坐标为
的直线上,因此设圆心坐标为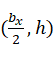 ,根据平面圆的标准方程可得:
,根据平面圆的标准方程可得:
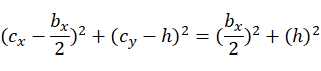
上式中只有h一个未知数,因此可解得:
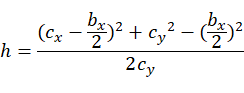
最后将圆心转换到空间坐标系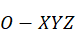 中,上面算得圆心为在U,V上的值,通过与U,V相乘并加上点
中,上面算得圆心为在U,V上的值,通过与U,V相乘并加上点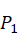 的偏置可求得圆心在空间坐标系中的坐标,半径通过其中一个点求取与圆心距离即可。
的偏置可求得圆心在空间坐标系中的坐标,半径通过其中一个点求取与圆心距离即可。
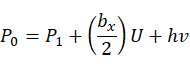
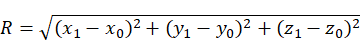
注: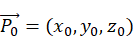
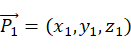
圆弧插补的实现流程为:将空间点转换到三个点形成的平面,将三维问题转换为二维。然后计算圆弧角,并在该平面上进行插补。最后通过变换矩阵,将插补点从二维坐标转换为三维坐标。
空间圆弧本质上是三个空间点形成平面(平面M)上的圆弧,我们只要求出坐标系在坐标系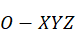 下的变换矩阵T,就可通过坐标变换将三维空间(
下的变换矩阵T,就可通过坐标变换将三维空间( )的圆弧变换到二维平面(
)的圆弧变换到二维平面(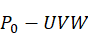 )的圆弧。
)的圆弧。
由平面方程可算得平面M的法矢量的方向数为:
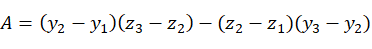
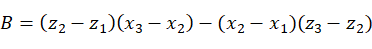
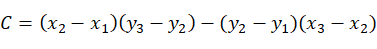
以平面M的法矢量方向作为新坐标系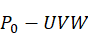 的W轴方向,W轴的方向余弦为:
的W轴方向,W轴的方向余弦为:
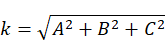
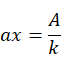
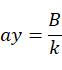
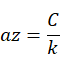
以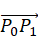 方向作为新坐标系
方向作为新坐标系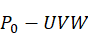 的U轴方向,U轴方向余弦为:
的U轴方向,U轴方向余弦为:
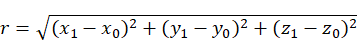
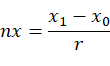
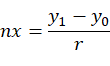
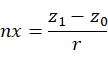
以U轴方向余弦与W轴的方向余弦的叉乘作为新坐标系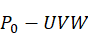 的V轴的方向余弦,V轴的方向余弦为:
的V轴的方向余弦,V轴的方向余弦为:
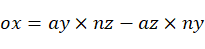
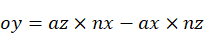
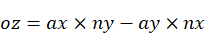
可求出新坐标系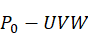 在坐标系
在坐标系 下的变换矩阵
下的变换矩阵
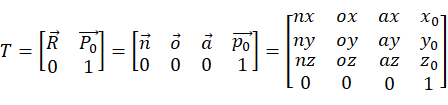
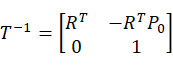
进而可求出P1,P2,P3点在新坐标系下对应的坐标值,其中i=1,2,3
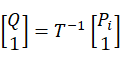
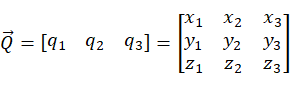
在实际机械手的空间圆弧的任务操作中,圆弧一般具有确定的插补方向,此处约定在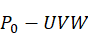 坐标系中UV平面内逆时针方向为其插补方向,即由P3到P2再到P1的圆弧始终为逆时针圆弧。
坐标系中UV平面内逆时针方向为其插补方向,即由P3到P2再到P1的圆弧始终为逆时针圆弧。
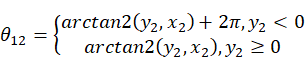
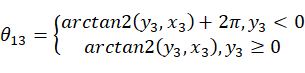
通过MATLAB搭建空间圆弧插值算法,得到结果如图2.5。
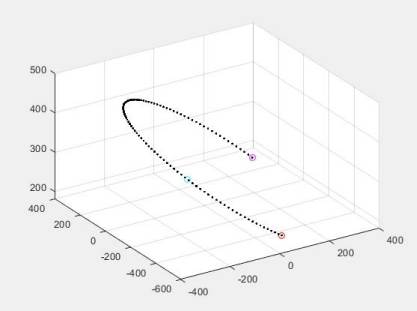
图2.2.1 经过插补得到的空间圆弧轨迹
借助MATLAB机器人工具箱进行机械臂笛卡尔空间圆弧轨迹动态仿真,结果如图2.5。
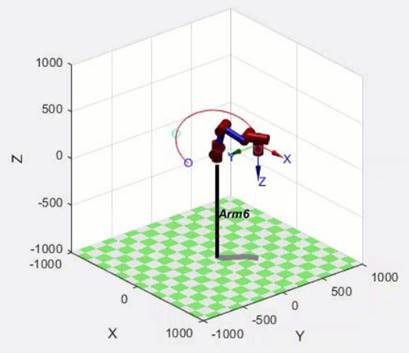
图2.2.1 笛卡尔空间圆弧轨迹规划仿真
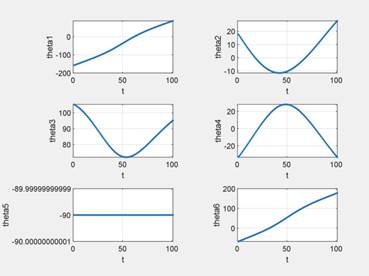
图2.2.1 笛卡尔空间圆弧轨迹规划关节角度变化曲线
本章小结
本章首先建立了机器人的D-H坐标,进行了UR5机器人的正、逆运动学求解,分析了奇异性位姿,通过搭建SIMULINK模型并与机器人工具箱进行比较,验证了推导及算法的正确性。针对动力学部分,运用牛顿欧拉法推导了UR5机器人的动力学模型,并在Simscape中建立了对应的物理模型。最后介绍了空间直线、圆弧曲线轨迹规划并运用MATLAB机器人工具箱进行了仿真。

